Time Delay through Inductor

Many people visualize current in a small loading inductor as starting at one end and traveling through the conductor turn-by-turn. It is this visualization that causes us to conjure up all sorts of untrue ideas of what a loading inductor does. One way to prove or disprove the perception current travels through the conductor is by examining time taken for current at one end of the inductor to "appear" at the other end. 

The sample inductor in this test is a typical 80-meter loading coil size. It is 100 turns, ten turns per inch, and 2 inches inside diameter. The wire is tinned number 18 buss wire, inductor Q measures 290 at 4 MHz. This would be an example of a reasonably good Q 80-meter loading coil.

We know many things about this inductor right away. We know conductor length making up the coil is about 53 feet. We know light travels at 982,100,000 feet per second in freespace. We know physical length is 10 inches, plus about 1 foot of total connection length in the test fixture. We also know the very fastest speed electromagnetic energy can travel is the speed of light in freespace, other things only slow it down.

If current winds through the conductor length, time delay should be about .98 nanoseconds per foot of conductor length. Time delay would be 54*.98 = 53 nanoseconds.

How long does it take current reach the other end of this inductor? Here's a plot of time delay at various with frequencies:

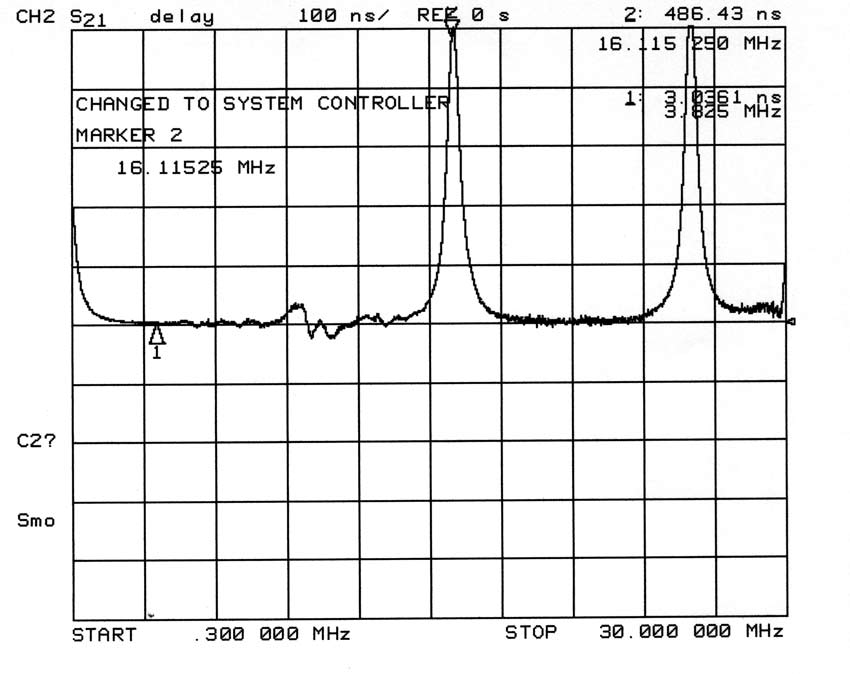
On 80-meters, and actually over a fairly wide frequency range, time delay is about 3nS. 3nS is equivalent to 3.06 feet of distance. We know 1 foot is occupied by the test fixture connections, so the ten-inch long inductor appears to be about two feet long so far as current propagation delay.

How does the current travel through the inductor so fast?

At first this seems impossible, but the  answer is actually quite obvious. Time-varying current gives rise to time-varying magnetic flux. This magnetic flux, since conductor spacing is close and the distance very small, links the starting turn very tightly to the next turn. The rapidly changing magnetic flux causes charges to move in the next conductor, and the changing magnetic field couples through all the close spaced turns with very little time delay. It is this magnetic flux coupling that provides the primary mechanism for energy transfer through the inductor, and the path is much shorter than the circuitous and much longer path along the conductor.

The above data corresponds to phase measurements showing phase delay in current is very close to zero electrical degrees.

Where does the coil gets it's well-known lagging current we read about? Very simple. The current at BOTH ends of inductor, when there is no capacitance present to correct the phase shift, lags voltage at the source end by a value that depends on system  resistance and the inductor's reactance! There is no magic involved in this at all. As a matter of fact, this all makes very good sense when we think about it. We know that a reactance looks like some value of reactance all through the system if an opposite reactance does not cancel it. This means voltage is out-of-phase with current, with voltage leading current at the generator. Current lags the generator voltage an equal amount at either end of the inductor, even though delay time is finite.

If the inductor in this test was an ideal inductor, time delay would be just under 2nS in this test system. Since it is less-than-perfect and does not have perfect flux coupling, time delay is longer (about double) we might expect.

Mobile and other Inductors Page

since 3/11/2006