Related pages Radiation Resistance

We tend to think of electric, magnetic, and radiation fields as physical "things"...much like an element would be in chemistry. This can cause problems!

One popular (but incorrect) assumption is we can combine, mix or blend fields into another field. After all.... we have electric fields...we have magnetic fields...surely we can mix them and create an electromagnetic field. This would have a distinct advantage, because we all know nearfield losses are higher than farfield losses. We know the farfield field ratio (or field impedance) is set by the media the wave propagates through. With reasonably dry air or vacuum, at normal radio frequencies, we know the impedance is 377 ohms. Why not just  mix the two fields and create the third field without all that needless nearfield loss? 

If, in our mind's eyes, we can mix fields the next logical step would be to conclude we can separate, filter, or sort the fields out whenever handy. If we have a problem with electrical interference, we can just eliminate the electric field. If we have a problem with field intensity  (defined as volts-per-meter) causing problems with the neighbor's VCR, we can reduce the electric field and cure the problem. After all, it is electrical interference, isn't it? 

We logically might assume, just by name, we can mix the various fields and make a new field. We logically might assume we can split the combined fields back apart if we don't like what is happening to one of them. 

Unfortunately, none of the above is true! The above conceptual problems started at the very beginning, because we assumed fields were physical things like building blocks. They aren't. 

Fields are really just mathematical descriptions of forces between charges. We have three simple conditions that create physical forces between charges. They are electric, magnetic, and electromagnetic (radiation) forces. They are all created by distinctly different physical actions in a system. We can't mix the various names for effects resulting from a certain physical condition and create a new cause! Fields describe the effects of certain causes, they don't create the causes of those effects!!!

Electric Field    

Electric field describes a force created by uneven charge distribution. Nature wants charges to be evenly distributed, she can only take so much piling up of charges in one spot! The force between charges, caused by nature trying to balance or even the distribution of charges, is called an electric field.  

Uneven charge distribution goes hand-in-hand with a voltage difference between two physical points. We can obviously can have a difference in charge distribution in insulators as well as conductors. A comb, "charged" by running through our hair (if we have any left), can have an electric field. The force of this field can pick up tiny bits of paper as nature tries to equalize the charge distribution. The terminals of a battery have an electric field between them and when we place a conductor in that field the charges try to equalize. Another example would be an antenna, where a voltage difference (uneven charge distribution) between two points creates an electric field. 

Any difference in charge distribution, whether the charges are "moving" or standing, causes a physical force. We name this effect an electric field, and describe it mathematically in volts over a certain distance (like millivolts per meter). This field (or force) decreases rapidly with distance.

Magnetic Field

Magnetic field describes a force created by moving charges. When charges are moving, they exert a force on all other charges around them. We call this effect the magnetic field.

One example of a magnetic field is a conductor carrying current. Perhaps it is a wire connected between two terminals of a battery. Another example would be a RF-current carrying conductor in an antenna. 

The movement of charges causes a magnetic field, and somewhere rooted in the creation of that magnetic field is an uneven distribution of charges causing an electric field!  Once again, this field (or force) decreases rapidly with distance.

Electromagnetic Field

An electromagnetic field is created whenever charges are accelerated. Acceleration occurs whenever a charge changes direction or velocity. When a charge accelerates, all the other charges in the universe feel a force trying to make them move. The only thing that stops that force from going on forever is when another charge (or combination of charges) accelerate to create an opposing force. We call the velocity at which this force or effect ripples through the universe the speed of light.    

One example of electromagnetic fields is in an AC current carrying conductor, like a power line. The time-varying voltage causes charges to move back and forth, and the change in velocity and direction causes the effect called electromagnetic radiation.

It is easy to see why our antennas have all three fields, and why we can communicate so well over large distances with low power. While the very strong electric and magnetic induction fields drop off rapidly with distance, the initially much weaker electromagnetic radiation field goes on until something cancels it. The radiation field allows us to communicate, not the electric or magnetic induction fields!

(Electric and magnetic induction fields store and return energy to the system, the forces from that effect are very strong, but they decay very rapidly with distance.)

Near the Antenna

Near any antenna fields are a complex mixture or " soup" of various effects from charges. When viewed from distances very close to the antenna, charges are almost always moving in multiple directions and distributed over vary distances from our viewpoint. It isn't always easy to picture or get a feel for what actually happens, especially when the area of the antenna is very large compared to the distance from which we observe the effects of charges. Near the antenna, pattern and field impedance is generally nothing like we might intuitively imagine! 

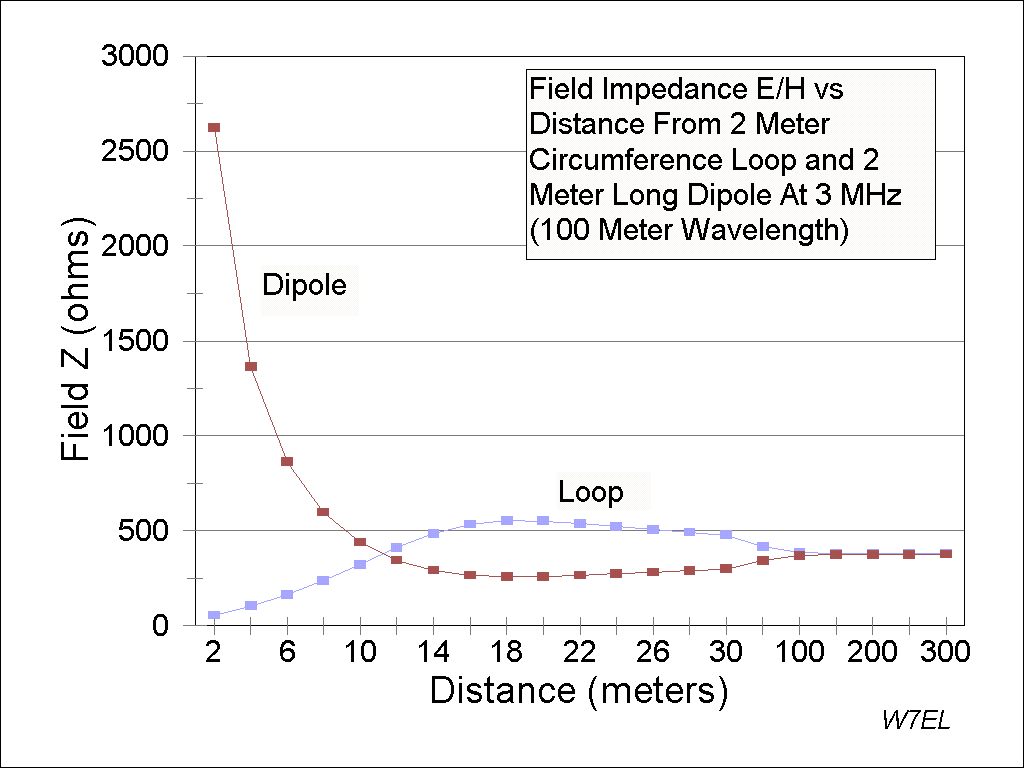
It is the response in this area, generally within l/10 distance from the antenna, that small "magnetic loop" and "electric dipole" antennas get their names.

Very close to the high-current area of a small loop antenna (but not near the capacitor end, because that is where the electric field dominates), the magnetic field dominates. Magnetic fields are mathematical descriptions of forces derived from moving charges, or current flow. This effect, when large compared to the electric field,  is sometimes described by saying the "field impedance" is "low". 

Conversely, near a small dipole or monopole with high voltage and little current, the electric field dominates. The largest force is from the very high open-end voltages, and very uneven charge distribution. We might say such an antenna has a " high field impedance" in the area where the electric field dominates any forces cause by moving charges.

In all of these cases, if the antenna is electrically small, the dominant fields apply only within approximately l/10 distance from the antenna!

As we move out further the weaker radiation field, because it is attenuated less with distance, starts to have a noticeable contribution to the charge forces. Because the phase of the fields (fields are a way of describing effects) is different at the antenna, the sum of the effects is different with distance. At some distance the low field impedance of a small loop becomes high, and the high field impedance of a small dipole becomes low!     

Since the distance of a wavelength in the above graph (thanks W7EL) is 100 meters, we can also considered the bottom scale as a percentage of a wavelength. We can see at about 11 percent of a wavelength (which would be about 50 feet on 160 meters), there is no field impedance difference between a small "magnetic" loop and a small "electric" dipole. At distances beyond 50 feet on 160 meters, the loop actually has a higher field impedance than a dipole.

Losses in the area around the antenna

The field impedance close to the antenna, when other than 377 ohms, has nothing to do with high losses near the antenna. Losses are directly related to the field density, and when we are close to any antenna the fields are very intense. Losses are not a field ratio problem, they are field intensity related. In very small antennas, virtually ALL of the losses are related to reactance canceling and resistive losses in the antenna and any lossy media around the antenna!  

We also must be mindful of the painful truth that we can not take either electric or magnetic fields to zero or all radiation stops. By definition, radiation is an electromagnetic wave. We can't modify the field impedance of an antenna without changing the voltage and current distribution of the antenna. 

Nearfield

The nearfield area is an area where the ultimate pattern is not fully formed, and where induction fields (from charge distribution and charge movement) have a noticeable effect on the forces we measure or observe. 

It is possible, with large arrays of small elements, to be out of the induction field region but still be in the area called the "nearfield" area or zone. Let's consider individual groups of elements as "cells", and the array a combination of small directional cells occupying a very large physical area.  Each cell has formed a radiation field. Depending on the size and type of radiator in each cell, induction fields that charge distribution plays a role in may be attenuated so much as to be negligible....yet the radiation pattern of the entire array may not be totally formed. The radiation pattern might not be fully formed even though the induction effects are no longer observable. We are in the nearfield, but not in an area where the energy storage fields have a noticeable effect.

This is the case with my phased Beverages and phased verticals. The individual antennas making up the array are so distant that the effects of charge distribution (electric induction field, sometimes called the electrostatic field) or steady movement (considered at one infinitely brief instant of time, or magnetic induction field) have no effect. For example, at about 1 wavelength distance the electric and magnetic induction fields are negligible from either my circle of eight verticals or 780-foot Beverages, yet the pattern of the overall array established by the phasing of multiple cells is not fully formed. The pattern would only be fully formed several wavelengths from each array, where the distance between cells or elements is only a small fraction of the distance we are looking back from.

The total pattern of two 780-foot long Beverages spaced 350 feet apart is not fully formed even at distances of several thousand feet, yet nearfield induction effects are totally gone at much shorter distances. The field impedance is established, yet the antenna pattern is not. 

The nearfield generally refers to or includes the area where "static" or induction fields still have a noticeable influence.

Fresnel Zone

The Fresnel (fre-nel, no "S" sound) zone is the area where pattern is still being formed. It may or may not include induction field areas.

Physically large arrays almost always have a physically large Fresnel zone. Even simple omni-verticals have a Fresnel zone extending out a few wavelengths. The field impedance may or may not have already been established in the Fresnel zone.

You may have heard about Fresnel zones during discussions of vertical antenna loss at low wave angles, or Fresnel lenses for lighthouses or other beacon lights. 

Farfield

The farfield is the area where any changes in distance result in no noticeable change in pattern or field impedance. Losses are lower in the farfield area because field density is lower, not because we call it farfield.

Summary

There really isn't a clear distance where certain effects just abruptly stop. Transitions are smooth and gradual, because transitions are the result of distance....nothing else. These regions of effects are all distance related, and caused by the three distinct effects of charges moving, charge distribution, and charge acceleration.

Even if we could somehow make the field-impedance a certain value or electric and magnetic effects a ratio equal to farfield ratio, it would not eliminate or in the slightest amount reduce nearfield losses! 

Losses are only related to the density of fields in any given media or environment, and nearfield or Fresnel zone losses decrease with distance because of the lower field intensity in any given lossy area as we move away from the antenna. At a greater distance, there is a wider cross-sectional area of lossy media carrying energy. The induction fields are attenuated greatly with distance. The field intensity and field density are both greatly reduced with increased distance. That is what reduces losses, not the 377 ohm field impedance.

Larger antennas, in general, have larger boundary areas for electric and magnetic fields. With wider boundary areas, the system has less-concentrated fields and charge effects. Very small antennas of any type obviously have very concentrated fields, and the high field density or concentration of current or voltage in conductors are at the root of increased loss. The concentration of energy in a small area is the real reason losses are generally much higher in smaller antennas, and this has little or nothing to do with field impedance! 

We can not mix fields and create a different field and make a small antenna become an "artificial large antenna", nor can we "filter" fields and remove the electric field to reduce electric noise.

This page has been visited times since June 12, 2004 

©2000-2006 W8JI