Rotating Mass, Available Horsepower, and Acceleration

We see or experience centrifugal force and inertia every day of our lives, and intuitively know how it works. One of the best examples is twirling a rope with a weight on the end. We know the faster and further out the weight is, and the heavier the weight, the further the weight will fly when we let go. This is because we store more energy in the weight as we move it faster, swing it in a wider circle, or use a heavier weight. The energy isn't really wasted, it is stored and released later.

Common Questions

If cluster gear weight of a transmission is reduced, how much will acceleration improve?

These questions can be answered if we know the weight change, the distance out from the center the weight change occurs at, the speed (RPM), and the time period over which the RPM change occurs. Even without exact calculations, we can get a feel for how things change. This will help us budget our money and make better choices, or at least have a feeling for what we are accomplishing.

Using readily available on-line calculators, we can understand how changes in rotating mass will affect available horsepower in a vehicle.

What does a rotating mass actually do?

A rotating mass does not really consume or dissipate energy. A rotating mass stores energy. The rotating mass eventually either returns energy to the system in a useful way, or something converts the stored energy to some other form of unwanted energy. The conversion might be with a friction, converting to heat. The energy stored might be helpful, like the smoothing of cylinder pulses in an engine flywheel. The energy stored also might not do anything at all, or the stored energy can even be harmful, reducing acceleration or braking.

Accelerating an unnecessary rotating mass requires energy, and the acceleration process saps some of the horsepower we have available to accelerate our vehicles. Reducing available horsepower affects acceleration in a very predictable manner, and the horsepower amount needed to spin something up gives us some feel for how important a part change might be.

Four things determine the effect of rotating mass. Every one of these things is important:

The above is very important. If we double the effective "circle size" the weight is rotating at, we get four times the stored energy. If we simply double the weight without changing the spinning radius, we just double stored energy:

We should carefully think about what this means when we change things. Some changes are worthwhile, some are not. We also cannot use carte blanche rules, like the silly rumor that reducing a rotating weight is like dropping the vehicle weight four times that amount. As a matter of fact, it is probably never four times. It is more likely closer to one, and might even be less than one!

Let's assume, just as an example, all of a wheel's weight is at the outer edge and remains at the outer edge. If we reduce a wheel's diameter but keep the overall weight the same, the wheel is a spinning ring with smaller diameter. The smaller diameter increases the wheel's RPM at the same vehicle speed. The smaller diameter also moves the spinning weight closer to the center.

Let's say we cut diameter in half. Now think about how fast the wheel spins. RPM will be twice what it was at the same speed. The half size diameter reduction spins the wheel twice as fast, and that would increase stored energy to four times the original amount if the weight was the same distance out. But the weight isn't the same distance out. The spinning weight is now half size. This 1/2 size reduction decreases stored energy by four times!

If we did not change the weight or weight distribution, and we reduced a wheel and tire diameter by half but drove the same speed, nothing would change. It would be a major change that just broke even. Moving the weight closer to the rotation center reduced stored energy, but the increased RPM to maintain the same speed increased stored energy the same amount. One cancelled the other, and stored energy did not change!

If we change tire and wheel diameter without changing weight distribution and weight in the tire and wheel, we don't change a thing. In this example, we gained nothing from a significant physical change. We also lost nothing.

Lightening the tire or wheel some distance out from the hub reduces stored energy. This is especially true if the weight reduction is far out from the center. If we change the weight one-pound fourteen inches out, it is like changing weight four-pounds seven inches out. Which brings up an important point we almost never hear mentioned, a lower weight part might not be lighter at the outside edge. It might be lighter in the center, where the weight reduction doesn't mean much.

It is more important to make something as light as possible on the OUTER edge, rather than near the (wheel) center. Spending money on smaller or lighter rotors to save rotating weight should be down the list, because the rotating weight is closer to the wheel hub. Unless the rotors are huge and we take weight out of the rotor's outer areas, things will not change much. (A light rotor and wheel is good for reducing un-sprung weight, and that helps keep our tires in contact with the road. It also reduces vehicle weight. But this is a different problem. Here we are talking about rotation, not the bounce inertia or "dead weight".)

If we spent money on the same weight reduction in the wheel, reducing weight out a little further away from the center, we would do much better. We would be removing weight further out from the center, where it does the most good.

If we spent our money on a lighter tire we would be getting the very most return for the weight change. The tire's weight change is mostly outside between the rim edge and the tread area. We get maximum effect from the weight change!

Think about this carefully. If we buy a lighter tire, we know for sure the weight comes off the most critical area. If we buy a lighter rotor, it is close to the center and, for the same weight change, the return is much less.

The wheels also speed up and slow down gradually. With an 11-second car, we have 11-seconds to speed the wheel up. Most of the horsepower pushed into the wheel and stored is pushed in near the end, when acceleration is least. Since we have more time to push the bigger amount of energy into the wheel, it takes less horsepower than we might expect.

Now let's think about a drive shaft. The driveshaft is a fairly thin hollow tube. Nearly all drive shaft weight is at the outside, since it is (of course) hollow. The shaft also turns at the same RPM no matter what the driveshaft diameter, because the RPM is set by the rear end ratio, tire diameter, and vehicle speed. If we make a driveshaft lighter and keep everything else the same, the vehicle acceleration change is often insignificant.

In the first place, the drive shaft is small in diameter. With a small diameter, less energy is stored for a given weight. In the second place, a driveshaft is really not that heavy. A steel Mustang driveshaft weighs somewhere around 30 pounds, so we just can't take that much weight out.

Also, the driveshaft spins up gradually and smoothly over a long period of time. It accelerates fastest at slowest speeds, and that is when it needs the least energy to spin up. Because it has a long time to spin up, is a small diameter, and because it does not weigh much, the driveshaft does not remove very much horsepower at any instant of time. Despite what we are told, a change in driveshaft weight has, at best, a very small effect on acceleration. Likely any change is immeasurable in a street/strip car.

Now a lighter shaft certainly can help in a very light vehicle. It can also help in a road race car (as will a light crank and flywheel), because road racing requires instantly changing from acceleration to deceleration.

A light driveshaft won't change anything significant or measureable in a 3000-pound 11-second car, except how fast dollars leave your wallet!

Another worry is driveshaft diameter. If we go from a 30-pound 3-inch steel driveshaft to a 30-pound 3.5-inch aluminum shaft, we move the weight out 3.5/3 = 1.167 times. That increases stored energy 1.167^2 times, or 1.36 times. If we store 0.3 horsepower in the shaft, changing the diameter will increase that to 0.4 horsepower. We would have to reduce weight 14.3% to 25.7 pounds just to break even with the diameter increase.

The worst thing about a driveshaft is the diameter is so small, and the acceleration time is so long, there just isn't much horsepower being sapped from the system. A typical steel driveshaft in a typical 12 or 13 second car only stores an average of about 1/4 horsepower. If we got 100% of that back with a zero weight shaft, we would never notice it.

Good reasons to change a driveshaft are to get rid of vibration and harmonic resonances in the shaft, to make it stronger, or to simplify a two-piece driveshaft system. The silliest reason is to speed the car up. Even if we only pay $100 for a shaft, it would typically be much less than 1/4-horsepower average gain. That would be paying much more than 100/.25 = $400 per horsepower. Paying a lot more than $400 per horsepower is not a good investment.

A flywheel can be fairly heavy, and the weight is a good distance out from the center. It spins at crankshaft speed, and it has to abruptly change speed (slow down) at every up-shift.

While a driveshaft stores around 1/4 horsepower spread over 12-13 seconds of time, the flywheel is entirely different. The stored energy in a 25-pound 13.5 inch diameter flywheel at 6000 RPM is something around 32,916 joule-seconds. This is 44.12 horsepower-seconds of power.

A 25 pound (400 oz) flywheel has about 32,916 joules of energy. Since each joule is one watt/second, and since 746 watts equal one horsepower, we have 32,916/746 = 44.12 horsepower-seconds stored. This would be one horsepower applied over 44 seconds, or 88 horsepower over 1/2-second, to reach 6000 RPM from zero.

An aluminum 12.5 pound flywheel would have half that energy, because weight is a direct one-for-one change in energy. If we ran it on a calculator we would see:

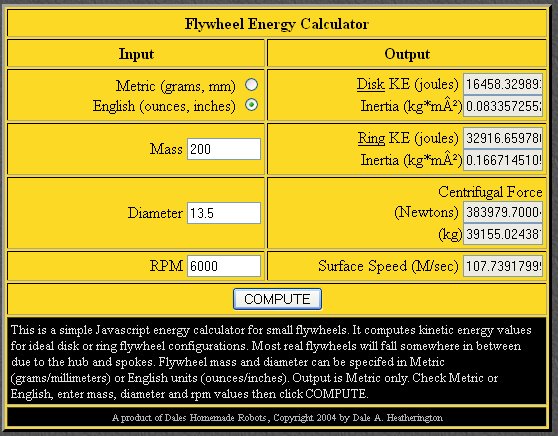
This is about 16,485 joules, or 22 horsepower-seconds of power. Before we run off thinking we will gain 22 horsepower by swapping flywheels, we have to realize this is horsepower-seconds . Also, the flywheel is NOT starting from zero speed!

If we launch our car at 4000 RPM, the flywheel starts at 44.4% of the 6000 RPM energy. (square of 4000/6000 times 6K RPM power) This is 19.6 horsepower-seconds with a steel wheel, and 9.8 horsepower-seconds with an aluminum wheel, of initial launch stored energy. We only have to add 12 horsepower-seconds to the aluminum wheel, and 24 horsepower-seconds with the steel wheel.

If we have two seconds to spin up to 6000, the engine will push either 6 horsepower average with aluminum, or 12 horsepower average with steel, into the flywheel. If we have 6 seconds to spool up, average horsepower is either 2 or 4 horsepower.

Also, not all of that stored energy is wasted. When we shift to second gear, the extra energy is returned on the shift. The engine gets a "boost" as the flywheel power is returned to the slower-turning transmission input shaft.

A car with street tires and traction issues will benefit from a heavier flywheel on launch, and be hurt more on the shift.

A car with good traction will benefit on the launch with the heavier wheel, but could loose a little power as it runs up through low gear.

Either way, we are not talking much power, and the results are highly dependent on the vehicle. We might gain ET or lose ET depending on many factors.

There are two general ways the flywheel affects acceleration, although this can vary. In a light car with very fast 60-foot times, a lighter wheel can slightly improve 60-foot times. This is because the launch is often at full throttle, the car generally has a steep gear, and we want to plant the tires hard into the track without encouraging spin. The tires hook hard, and usually have a very soft sidewall that absorbs shock. We want the engine to quickly match the RPM needed to move the rear wheels, and not overpower the available traction. It is a wide open throttle high-RPM launch.

A typical street-strip car is different. Generally we can't launch at wide open throttle, the tires are stiffer walled, the suspension is heavier, and things just don't hit as hard. We actually want a heavy wheel (and a heavy crank) to smooth out the power. This lets us have a much more controlled launch, and smoothes out any sudden application of throttle. An aluminum wheel, especially when the car is severely traction limited and heavy, can really hurt 60-foot times. A light aluminum wheel not only makes a street car hard to drive, it usually hurts at the track. It is especially bad with a heavy street machine.

Now that we have seen the flywheel in detail, we can compare it to the driveshaft. The flywheel is typically around 20-40 horsepower-seconds of energy, and has a somewhat small effect on overall power. The driveshaft has about 5.5 horsepower-seconds of energy, and has the full length of the track to spin up.

In a 13 second car, the driveshaft consumes about 1.5 horsepower maximum over the first sixty feet. If we cut the driveshaft weight in half with no increase in diameter, we would pick up 0.75 horsepower. If we increase diameter from 3 to 3.5 inches and reduce weight by 30%, we would just barely change the driveshaft's stored energy. The added diameter would increase stored energy 1.36 times, and the reduced weight would reduce stored energy by 30%. We would gain about 0.25 horsepower-seconds, or 0.02 horsepower average power gain over the track length with a 13 second car.

A crankshaft is a bit worse than a drive shaft. A crankshaft accelerates and changes speeds through every gear, so it is constantly storing and returning energy to the system. In low gears it spins up pretty fast, spinning up from "launch" RPM to shift RPM. This spin up repeats at every shift. The crank also has to be heavy to support the pounding and tugging of the pistons and rods as they accelerate and decelerate, so we are dealing with some weight.

Fortunately the crank diameter is small. A 3-inch stroke requires only a 1.5-inch throw radius. Unless we make a huge change in OUTSIDE weight in the counterweights, in most engines making the crank lighter makes very little sense. The dumbest thing to do is hollow out the crankshaft center because it is the smallest rotating diameter area. Don't believe this? Download the following technical paper from the Scat Crankshaft website. Lightweight Crankshafts- Performance or Deception

Scat has it 100% correct. Many bench racers, and even some crankshaft manufacturers, exaggerate a good bit! They remove weight where it makes little difference in stored energy, but might make a difference in strength. Some transmission experts worry about the wrong thing also. If we worry about the outside edge weight of the largest-diameter fastest-spinning parts that speed up and slow down at every shift, we are worrying about the correct parts. If we worry about parts that speed up at the rate of the driveshaft, we would be wasting our efforts.

The purpose of the examples was to give you a feel for what to look at first. Any weight reduction is good for horsepower to weight ratio, but some weight reduction has a bigger payback. Things that change speed often, change speed rapidly, and/or are heavy at a large distance out from the center...make the most difference. Look there first.

The last "things" to worry about are small diameter "things" that change speed a smaller amount, change speed over a longer time, and change speed less often. They will have much less stored energy. If we want to reduce rotating mass we should look at the heaviest things that speed up and slow down most often, spin the fastest, and are large in diameter with most of the weight at the outside edge.

Why do things work this way?

First we have to understand what power and energy are, and what rotating mass does with that power or energy. Contrary to popular belief, rotating mass does not consume energy. A rotating (or moving) mass stores energy. This effect is very much the same as pouring energy in a bucket, much like charging a capacitor in an electronics circuit. Virtually all of the stored energy, except for that lost by conversion to heat, is still there and available to do work at some time in the future. That future where energy is returned might be milliseconds later and help us out, or it could be some considerable time later and waste energy. This is why time is very important.

One example of useful energy storage is the flywheel and crankshaft of a car. The force on the crankshaft is in pulses. A common four cycle V8 has four power cycles per crankshaft revolution, and there are 100 turns of the crank per second. At 6000 RPM an 8-cylinder 4-cycle has 400 power pulses per second. The flywheel (along with the harmonic dampener and weight of the rotating assembly) smoothes these pulses out by storing and releasing the pulsed energy from the explosions in the cylinders. The result is a smooth rotation that will not tear gears up, vibrate the car, or beat on bearings.

We should always remember rotation, or movement of a mass, does not actually destroy energy. If it did, the earth would have stopped spinning millions of years ago! The key to understanding how weight changes affect performance is to understand some very simple basic energy flow in the system.

Definitions:

Energy

Energy is the capacity of a physical system to perform work. Energy exists in many forms like heat, mechanical, electrical, and others. According to the law of conservation of energy, the total energy of a system remains constant. Energy may be transformed into another form, but it is constant within a system.

For example, we all know two pool balls eventually come to rest after colliding. They stop moving only because the applied energy (from moving the cue stick) is eventually converted to heat (from friction with air and the table) and sound (which is not very much of the energy loss). The ball movement along the table's felt surface and through the air transfers energy outside the two moving balls to the air and environment around the table and into the table itself. The temperature of the table and air rises ever so slightly, because the applied energy moves outside the system we "see"! Since the heat energy is spread all around in a very large area, we don't notice the temperature rise. We just notice the balls quickly quit moving.

Another example is our car's brakes. The energy stored in the moving weight of the car is converted to heat by friction of brake pads rubbing against metal rotors attached to the rotating wheels. This converts stored energy (the engine put into the weight of the vehicle) into heat, and the heat (containing all of that energy) radiates out into the air. Most of what we actually do in a car is move heat around.

Newton's first law

A mass continues in its state of rest, or continues uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.

Old guys like Newton sure had a lot of time on their hands to think about simple things, but they got it right. A rocket coasting through outer space is a good example. It will go on forever in a straight line unless it hits something, or unless gravity or some other force pulls it in a new direction. The earth wants to move in a straight line, except gravitational attraction to the sun bends its path constantly. A bullet reacts the same way, except friction with air and gravity changes the direction and speed gradually over distance.

Newton's second law

The acceleration produced by a particular force acting on a body is directly proportional to the magnitude of the force and inversely proportional to the mass of the body.

We push harder and/or longer, and something moves faster. If it is heavier, we need to push longer or harder (or both) to obtain the same speed. It takes more energy to accelerate a heavier object to the same speed as we might move a lighter object to that same speed. We can either apply more force or apply the same force over a longer time to make something move faster. It is all about TIME times the POWER, or the amount of TIME an amount of POWER is applied. This is why those big showoffs can eventually move a large boat, a railroad car, or an airplane. All it takes is low friction and enough time and someone who can't move a Volkswagen with two flat tires can roll a 10-ton railroad car.

Acceleration, Energy, and Power

Acceleration, by definition, is a change in direction or speed. If we slow something down it is acceleration, just in a negative direction. If we turn a vehicle or any other mass in a new direction, it is really acceleration at a new angle or in a new direction. This is why we can compare or define braking and cornering in G-force (g's), just as we do with "taking off" acceleration.

We apply force (and this means we apply energy) over time (force applied over time is power) to accelerate an object. If we want to spin a top, we apply force off-center from the axis and at right angles to the axis. The top stores the energy we apply, and continues to rotate. Over time the stored force is converted to heat from friction and the top gradually slows until it finally stops.

Force is pressure or energy. The product of the time we apply the force and the amount of force is the power. Power over time is a very useful thing to us because it means we can do work with it. Power alone, without time it is applied, is not not so useful. Let me give some examples:

"Watts" are a measure of power, much like horsepower. "Watts" alone are not speed, because a watt does not include a defined application time. A watt is only power level, or work level, of energy over an undefined time.

If we include one hour's time we would have a watt-hour. Kilowatt-hours, watt-seconds, watt-hours, and other combinations of power level and time define electrical energy or work. This is why we billed for kilowatt-hours at our homes! If we were billed for plain old "watts", it would not tell anyone how much "work" we bought. Watts are a true scalar (single dimension) measure of ability to do work, just as horsepower is. Both indicate a force or the ability to do work, but both lack any inclusion of work time, so we have no idea how much work was done, or could be done.

Horsepower is a function of RPM and torque, just like watts are volts times amperes. Horsepower is an ability to do useful work, but doing actual work requires time. Torque is pressure, and since it does not include speed it is not a very useful measure of system power or the ability to accelerate or move weight. Despite what we hear, crankshaft torque is not directly related to moving something off the line or pulling a heavy load. Up at the engine, it is really all about horsepower. The horsepower (torque at a certain RPM) is eventually converted through gears and other mechanical devices to a new torque value at a different RPM. Eventually all we care about is the rotational pressure on the contact patch of our tires that thrusts our car forward. A 800 lb/ft torque at 2000 RPM engine does not accelerate a vehicle as well as a 400 lb/ft engine at 5000 RPM, because horsepower is a product of torque and RPM. The higher RPM engine can be geared to provide more forward pressure at the wheels. The higher RPM engine, with less torque, has more horsepower.

If you notice, ET calculators don't ask for torque. This is because torque does not quantify the ability to do work. ET calculators ask for horsepower, because horsepower clearly defines an ability to do work.

Joules are another common measure of ability to do work. A joule includes both time and force (pressure). A single joule is one watt-second, or the equivalent of one watt applied for one second. A single joule could be 10 watts applied for 1/10th of a second (10*1/10 = 1), the product of time and force only has to be ONE watt-second to make one joule. If we applied TWO watts for 1/2 second, we have the same work. Two watts for 1/2 second is one joule (2*1/2=1).

Horsepower can also be stated in kilowatts. One horsepower is approximately 0.7457 kilowatts, or 745.7 watts (the exact value is 0.745699872 kilowatts). This means 746 watts for one second is 746 joules and that is one horsepower-second! One kilowatt is 1.341 horsepower.

Many European engines are rated in kilowatts instead of horsepower, you've probably seen that. A 300-horsepower engine would be about 223.7 kilowatts. Your house probably consumes between 2 to 5 kilowatts of average power, depending on how large it is and how you heat or cool. This is somewhere between 2-1/2 to 7 horsepower of average power. Think of what would happen to the power grid if we converted all our cars and trucks, like the Greenies want, to run on electricity! We would run out of electricity very quickly.

How many joules are in 1492 watts when applied for 1/2 second? 1/2 times 1492 or 746 joules! 746 joules is one horsepower-second. We could rate our engines in joules if we needed to include both power and time.

Horsepower and Acceleration

We know horsepower alone is not a measure of useful work results, we must know the time a certain horsepower is applied (or removed) to know how it affects acceleration. Fortunately there are horsepower calculators that predict ET for a given power. These calculators work because they know the distance, they know the applied horsepower (they assume it is constant), and from that they can calculate speed and elapsed time. They do this because they assume the power is applied constantly and they calculate the speed change over time. From the speed and time, they get the distance. When they see 1/4 mile (or 1/8th mile) they stop calculating and display the speed and the time taken to reach that speed and distance.

Now here is an interesting thing. It takes a certain number of horsepower-seconds (certain energy applied) to reach a certain speed for a given weight. If we make the vehicle twice as heavy, it takes twice as many horsepower-seconds (twice as much energy) to go the very same speed.

Now let's apply 100 HP to go 1/4 mile in a 1000 pound vehicle. We went 108.6 MPH in 12.55 seconds. Now let's say we have a 2000 pound car. To have the same speed and time, we have to also double the applied force. If we apply 200 HP in our 2000 pound car we have exactly the same ET and MPH! Now we know why insurance companies, in the late 60's, often limited insurance to a car with 10:1 weight to horsepower ratio or more. They didn't care if it was a 4,400 pound Super Bee Dodge with a 425 HP hemi or a 315 HP 3200 pound Hurst Rambler Scrambler, the insurance companies wanted weight to power over 10:1 ratio or you could not buy insurance. 10:1 weight-horsepower is at very best a 108.6 MPH at 12.55 seconds car! My American Motors 10:1 Weight-HP Hurst S/C Rambler, as a documented fact, set a new national ET record of 12.54 seconds in the 1/4 mile back around 1970.

Let's say we want to change the drive shaft rotating mass to improve power available to the rear wheels. We all know most of the weight in a driveshaft is at the outer edge. It is a hollow tube. Let's say the original shaft weighed 30 pounds, and we want to change it to a 15 pound aluminum shaft. The drive shaft is 3.5 inches in diameter.

We can go to another calculator to find the joules stored in the driveshaft! When we know the joules, we know the horsepower-seconds sapped from moving the car. Let's say the engine peaks at 6000 RPM at the end of the 1/4 mile, and that took 13 seconds.

The original driveshaft weighed 30 pounds and we had to spin it to 6000 RPM. If we input that, we see it consumed (and stored) 5310 joules. 480 ounces in a 3.5 inch diameter RING (hollow center) and 6000 RPM.

That is 5310/746 = 7.12 horsepower-seconds to spin the shaft to 6000. Since the time was 13 seconds, the shaft soaked up 0.548 horsepower distributed over that 13 seconds.

Now we change to the aluminum shaft. Everything is the same except the weight, it is now 15 pounds or 240 ounces. Using that flywheel calculator we find we used 2655 joules. This is 2655/746 = 3.56 horsepower-seconds. Over 13 seconds, we "stored" .274 horsepower. The net gain in available energy over 13 seconds was about 1/4 horsepower.

If we are spinning up a very large diameter mass, or a very heavy mass, and we do it rapidly, we sacrifice a lot of available power. If we are spinning up a very small diameter mass, especially over a longer period of time, we give up less power at any instant.

The change from an aluminum flywheel to a steel flywheel is much more pronounced than the change of the same weight in a driveshaft because the aluminum wheel is much larger in diameter. We also speed and slow the flywheel as we accelerate and shift, instead of smoothly spinning the thing up like a driveshaft.

The truth is for drag racing, unless we have a God-awful fast car or a road race car where we have to instantly change power, an aluminum wheel barely makes a perceptible change over a steel flywheel. The aluminum wheel can actually be slower in a drag car, because the applied power is not as smooth. It is harder to get a light aluminum flywheel out of the hole, and that can easily offset any small "available power" change.

Summary

This is an approximation designed to give you a reasonable feel for how a change in rotating mass affects acceleration. We can see the power extracted to spin a weight up is not very much if we do not spin it up too quickly, or if what we spin is not very heavy and/or very large in diameter. The "feeling" most people cling to (and parrot) is that "heavier rotating mass kills acceleration". This is generally not true at all for big heavy cars, although it can be true. Most things we fret about make no appreciable difference in the grand scheme of things. I would never bother changing from steel to an aluminum driveshaft in my car, because my car takes 11 seconds to go 1/4 mile. The car weighs 3000 pounds, and this means I might save 20 pounds of weight and 1/2 horsepower lost to spinning that weight over the length of the track. $400 is not a good investment at all for 1/2 horsepower over the length of the track, or the extra 1/2 horsepower applied for 11 seconds I have to extract at the end and convert back to heat with my brakes.

I don't really have to worry about how fast things spin up at this point. I don't care if the crank is 12 pounds lighter out of 50 pounds. I don't care if the driveshaft is 15 pounds lighter out of 30 pounds! Right now that $400 to $1000 would go a lot further if it made 20 more engine horsepower, or removed 60 pounds of static weight. When I start running out of easy power, then I will spend money making expensive things lighter. The big problem right now is traction, so right now I want to smooth the power out. The last thing I need is to make the car more critical for launch RPM by using a lighter flywheel or shock the tires more by using a lighter driveshaft. The first major weight reduction will be the front K members, because that would remove weight from the front and effectively add a larger percentage of weight to the rear wheels! The last weight reduction for my car will be an aluminum flywheel or driveshaft.