Related pages:
Mobile antenna FS comparisons Loading Inductors Inductor Spice Model
W7EL's Measurements and comments Constructing an RF Current Meter
| Note: the discussion below primarily deals with loading inductors used in mobile HF antennas rather than long radiating helices. If you read carefully you will see why a long helice behaves more like a radiating transmission line and less like a conventional inductor. The discussion below also applies to tank coils. It is important to read everything below IN CONTEXT for yourself and not listen to what other people tell you it says. Some people, for some reason I can't understand, claim it says things that are not actually said. :-). Don't depend on other people's reading skills. |

How Does an Inductor or Loading Coil Work?
Much of the data below also applies to inductors in equipment, such as tank circuits.
The most common questions are:
What does the coil do? A normal physically small (physically small compared to antenna length or wavelength) loading coil or loading inductor does not replace a missing fraction of a wavelength. A physically small loading coil simply inserts a series inductive reactance that cancels capacitive antenna reactance. When a 150-ohm reactance inductor is inserted in series with a 150-ohm capacitive load (like an antenna) reactances cancel. Only the resistive parts remain.
What determines current distribution in a loading coil? Current distribution is determined by stray capacitance to the outside world and the impedance terminating the loading coil. The current in any inductor would be equal at each end except for displacement currents. Displacement currents are "imaginary currents" that flow through a capacitance. A changing electric field is tied to these currents.
How much level difference is there in loading coil current entering the coil and loading coil current exiting the far end? If the antenna beyond the coil has low self-impedance compared to the impedance of stray capacitances that shunt current from the coil to "ground", currents at each end of the coil will be essentially equal. The current taper effect is not caused by the "missing antenna length" the coil replaces. Current taper is determined by the ratio of termination impedance to stray capacitance from parts of the coil to surroundings. If the portion of antenna above or beyond the loading coil is long or has a large physical area compared to the physical size of the coil, coil current will be essentially equal throughout the coil and at each end. In tank circuits, inductor current is equal at each end unless the tank capacitors have a very low value compared to the tank inductor's stray capacitance to the chassis. This is one reason why we do not want to mount an inductor close to sheet metal.
What does significant current taper in the loading or tank coil indicate? Large differences in end currents on an inductor are strong indicators of poor antenna or tank circuit layout or design. An example would be a situation where a loading coil or tank coil has high stray capacitance to other areas of the system (like the groundplane or surrounding objects) compared to capacitive reactance of the system at the high impedance ends of the inductor. Significant current taper indicates poor inductor, layout, or antenna construction or design.
click to view typical installation measurements
The Difference Between a Loading Coil and a Normal Inductor
There really isn't any difference between a loading coil and a conventional inductor or coil used in other systems, except the impedances and surroundings are different. The inductor or loading coil behaves the same way whether the load is a radiating antenna or an electronic circuit. An inductor is an inductor, it doesn't change characteristics depending on end-use, although different designs can work better with different reactance and circuit requirements.
Mobile loading coils or loading coils for short antennas often have very high reactance. They often have extremely low capacitance at one end, and this makes stray capacitance throughout the inductor a concern.
Stray capacitance from turn-to-turn increases circulating currents. Turn-to-turn capacitance increases effective inductance and effective resistance, yet at the same time unnecessary stray capacitance reduces system bandwidth and (contradictory as this sounds) also reduces effective Q.
Stray capacitance to the outside world causes the coil to behave like an L-network, and transform impedances instead of providing a pure series reactance. This is why the optimum form factor of a coil becomes longer compared to the diameter with any inductor having very high reactance. This is also why inductors (RF chokes), at high enough frequencies, behave like back-to-back L networks. We call this effect "series resonance" when discussing power amplifier plate chokes.
Inductors with low inductive reactance are much less critical of internal and external stray capacitances. Optimum form-factor in a low reactance inductor leans towards a short coil with the diameter nearly equaling length. In tank circuits, or with loading coils used with longer antennas or with capacitance hats, the optimum inductor shape becomes shorter and larger in diameter. In a short mobile antenna or very high impedance tank system or circuit, optimum inductor form factor becomes longer when compared to diameter. Long high inductance coils are generally good, compact large diameter inductors often work better in low inductance ranges.
Most optimized-form air core inductors fall between 1:1 and 4:1 length to diameter ratios, the exact value depending on inductor and terminating reactances. A coil behaves the same way regardless if used as a loading coil or used as a tank inductor.
Common myths about inductor behavior:
One common myth is loading coil current is reduced by standing waves or by the fraction of "electrical degrees" the inductor "replaces" as it passes through the length of wire in the coil. There are two reasons cited for this. One idea is the current is reduced because the loading coil replaces a certain amount of "electrical degrees" of antenna area, substituting or replacing the normal current taper seen in an unterminated antenna. The other idea is that series loss resistances cause a current reduction.
We often find inexperienced builders of 5/8th wl antennas think the "loading coil" needs to contain 1/8th wavelength of wire in order to make the 5/8th wave antenna a "3/4wl resonant antenna". They think, through wire length alone, the wire creates a low feed impedance by making the antenna three-quarters of a wave long electrically. In other cases claims are made one half-wave of wire wound on a compact form causes a 180-degree current delay, making a compact coil useful for phasing in a collinear array.
The basic flaw is the above ideas do not account for what actually occurs in a coil. The flawed viewpoint is current goes in one end, winds its way around through the physical length of wire in the coil, and after a time delay caused by the copper path length current appears at the other end. There is a physical mechanism that prevents what we might intuitively think happens from actually happening. A coil or loading inductor has magnetic mutual coupling between turns. The physical mechanism is the magnetic field in the coil!
What Really Happens
When current flows in the transmitter-end of the coil, a magnetic field is created. This time-varying magnetic field causes charges in the other turns to instantly move. This effect ripples through the length of the coil at light-speed, just over 186,000 miles per second. As long as the magnetic flux coupling is high, the delay through the coil is the speed of light over the physical length of the coil. In an inductor with good flux coupling from end-to-end, the electrical time delay in current is very close to the physical length of the coil expressed in degrees at the operating frequency. Note that this time delay is NOT the phase relationship between voltage and current, but the delay time of current appearing at each inductor terminal. More on this appears later in this text.
(Another interesting effect occurs. The increasing magnetic field sets up an "opposing voltage" as it cuts across conductors. This opposing voltage, created as the field expands, is what causes the current to rise slower than the applied voltage. If the exciting voltage is decreased the field collapses, and now the voltage changes polarity and aids current flow! If we don't allow the current to flow, the voltage will rise until it does. This is what causes the kick in a relay coil when we open the relay coil path, or the spark in an ignition when the points abruptly open.)
In an RF system, the physical size of the coil actually does add some "antenna effect". For example, on 160 meters the wavelength is about 550 feet. 1.5 feet is about one electrical degree. A skinny one foot tall coil, with negligible stray capacitance, would have about 0.67 electrical degrees phase delay of current between each terminal. This delay occurs because to coil occupies a physical length of .67 degrees. Current at each end would be almost perfectly equal, the taper would be about what we would expect for a fractional-degree-long coil.
(In the real world, all components have some stray capacitance and flux leakage, so they have a different amount of electrical length and current taper than the "negligible capacitance" case. In good coil designs, the capacitance and leakage is small and can be ignored. I'll show you measurements later to prove this.)
Now let's look at an extreme case. If the entire antenna is "coiled", like a helically wound antenna with no top hat or stinger, current would be reduced to nearly zero at the open end. This is because distributed capacitance over the length of the antenna is fairly high, the shunting capacitance has a low impedance compared to impedance at the end of the antenna, and current is diverted to ground in the form of displacement currents. The significant displacement current distributed along the coil causes phase delay through the coil, as well as the current taper along the length.
Compact loading coils are another matter. In many cases phase delay is negligible or immeasurable by normal methods.. providing flux coupling is nearly perfect. A good example would be a relatively compact toroid or a compact nearly-square L/D ratio loading inductor. I've found it impossible to measure the current taper in a toroid and very difficult to measure in a compact air-core loading coil. (The opposite extreme would be be a perfectly straight wire with no folds or bends or the helical antenna described above.)
In the case of the toroid or compact coil, the behavior would be such that doubling the turns nearly perfectly quadruples inductance. If we doubled turns and inductance simply doubled or increased at a much faster rate, we should know the coil is in a mode other than a pure inductor mode. This is a strong indicator inductor operating Q is less than optimum, and the inductor might behave less than ideally in critical applications.
As a matter of fact, observing inductance change while adding turns can be an excellent test for flaws or shortfalls in system design. A linear increase in inductance when adding conductor length indicates design problems.
A perfect impedance squaring effect indicates minimal electrical phase-delay, or "antenna length" of an inductor. Impedance squaring as turns are doubled indicates the undesired inductor stray capacitance has a high reactance compared to the antenna system beyond the loading coil. Of course there can be exceptions, but it is a good general rule that large current taper indicates the loading system is much less efficient than necessary.
Making a Delay Line
It's certainly possible to make a delay line from a coil without opposing fields caused by a second parallel conductor (a transmission line), but doing so requires stray capacitive reactance to be significant compared to the value of distributed inductance in the coil. It also requires significant flux leakage. This would occur in a very long helice, a very large diameter helice or loop, or an inductor near or wound around a large metal counterpoise or ground plane.
It's important to remember unless a coil is "stretched out" or "expanded" a great deal, the phase delay will not even be close to the physical conductor length. (The exception could be if you had so much capacitance the inductor acted like a series connected string of L/C/L networks as shown below).
In any case while this effect might be good in a collinear antenna or plate choke (assuming you do it right) it is a BAD effect in a short loaded antenna!
Inductor E/I Phase shift
An inductor delays the flow of current in relationship to applied voltages as the magnetic field inside the coil expands. Voltage increases before current starts to flow. This phase relationship between voltage and current is often confused with time-delay phase in the inductor. Say we have this simple circuit:
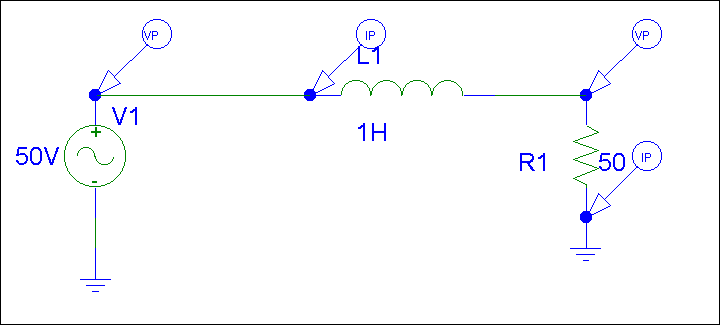
Current and voltage at V1 will be out-of-phase by the effect of L1 "charging" with magnetic flux. Current appears AFTER voltage rises, and falls after voltage falls. Current in R1, however, is exactly in phase with voltage across R1. That's because the voltage across R1 is always E=I*R.
Every component must follow the Laws or electrical rules established for that component.
The current in R1 is delayed from VOLTAGE rise in V1 by the voltage to current phase delay of L1. This does result in a time delay in relationship to voltage rise at V1, but there is NO current time delay through L1! V1, L1, and R1 all have the same peak current at the same time!!!
The notion that antenna loading coil delay current by the same time as they delay response to increased voltage is obviously nonsense.
Here is a graph of phase delays in the above system:
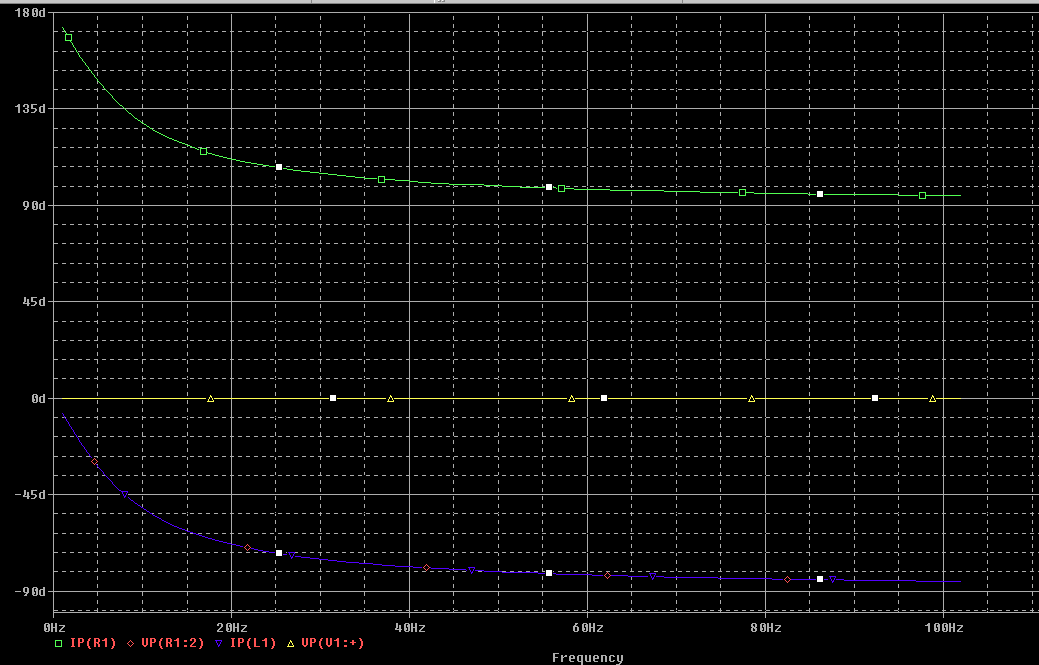
Current in the load, generator, and inductor all exactly track in the same relationship from dc up. There is no "phase delay". The generator voltage is a straight line different than current, and this indicates the generator sees a "reactive load".
This is an ideal model. It does not include shunt capacitance, or flux leakage.
Phase Shift of Current
What happens to current passing through an inductor with very tight inter-turn flux coupling?
Magnetic flux links the ends of an inductor. Current does not enter one end of the inductor, wind through the turns, and appear with a time delay related to conductor length on the other terminal. The magnetic field travels through the coil at light speed, and when the very first turn is magnetized every turn linked by the flux immediately has current induced. The delay is related to the speed of light and physical distance from the starting turn to the ending turn. (This assumes negligible stray capacitance to the outside world compared to load impedance.)
Here's a SPICE model of an inductor (this would represent perfect coupling) showing current at three points indicated by A, B, and C:
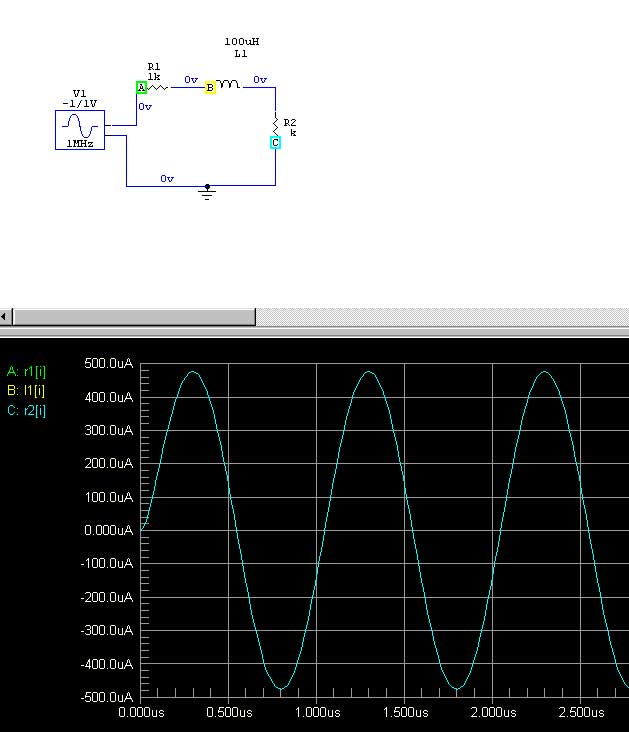
You can see A, B, and C have the same current and same phase. This would be true for forward waves as well as reflected waves. Of course this is an inductor with perfect mutual coupling and no displacement current. A real inductor of reasonable form factor would have some small phase delay.
Phase Shift Of Voltage
Where does the phase delay come in? The voltage at different parts of the system is delayed. Here are voltage waveforms with respect to ground:
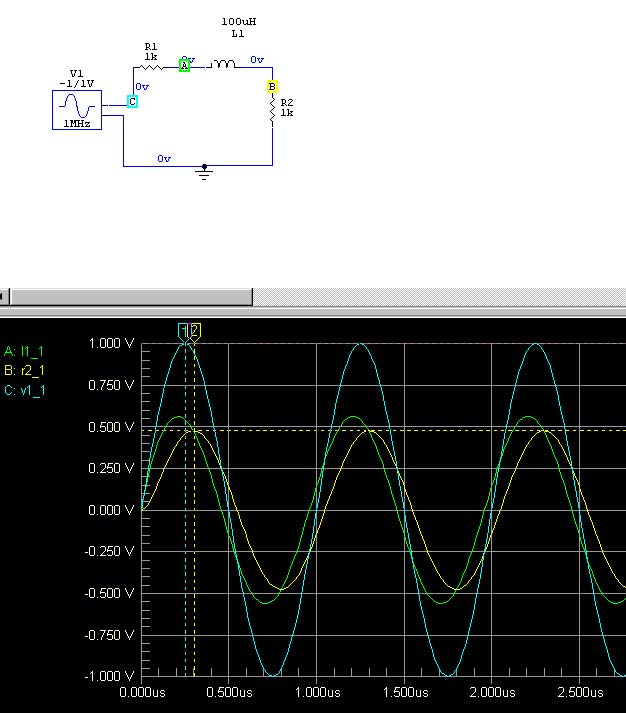
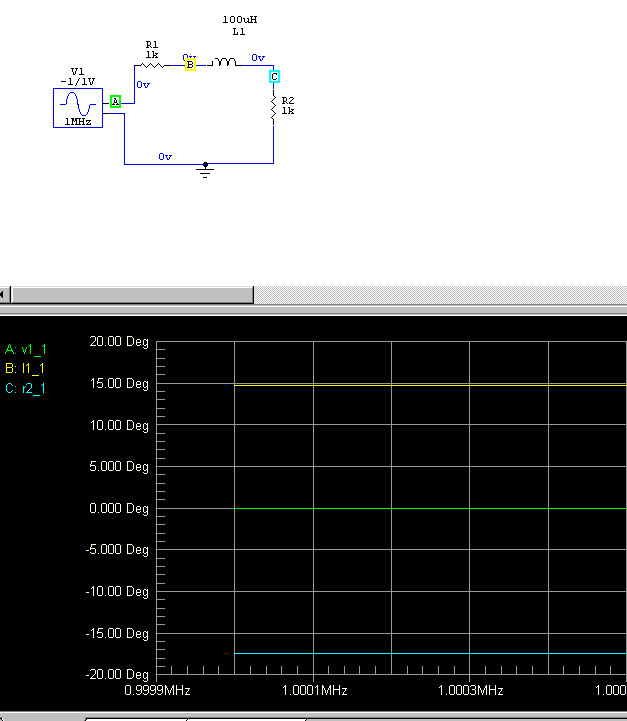
Spice allows us to show phase difference between multiple points. The graph to the left shows phase difference at three points.
The Misplaced Notion
Proponents of the idea that coils replace "antenna length" and equal the missing antenna length in degrees are unable to define a set of rules or logically demonstrate why a current reduction and "electrical-degree" phase delay directly related to the antenna area "replaced" occurs in a two-terminal component. While a long inductor with poor flux linkage from end-to-end, or an inductor with low values of stray capacitive reactance to a groundplane compared to series impedance, can cause SOME current inequalities and phase delays, the amount is normally immeasurable with normal thermal current meters when the inductor has good form factor and reasonable termination impedance above the coil. The amount of current taper actually rivals the disturbance of the system by adding the measurement device, unless we construct the measurement device very carefully.
Both W7EL and myself made independent measurements of current in small loaded antennas. These measurements demonstrate the "missing electrical degrees" in an antenna has nothing to do with current distribution in the coil. Some people have actually incorrectly reported W7EL's data! Here's what he had to post on rec.radio.amateur.antenna to correct misrepresented claims.
The Need for a Measurement
An article long ago on E-ham claimed measurements proved a new concept about loading coil current. The E-ham article put forth an idea that current disappears as it moves through a loading inductor without a mechanism like displacement currents providing a path. This claim conflicts with established component behavior, so it would indeed be fascinating if it were true! One of the claims supporting the idea that coils in antenna work differently than coils in circuits was that a non-radiating toroid loading inductor showed a current taper when used in an antenna.
I recently constructed a calibrated current meter that slips over whip antennas and masts, and is for all practical purposes totally immune to variations in voltage in the system. It also is mostly plastic, and has minimal effect on stray capacitance of the antenna. The resonant frequency and currents are not significantly perturbed by measurements with this meter. When I added a similar meter used in the other tests, resonant frequency shifted significantly! This is a sure sign the meter's capacitance or inductance is affecting the system.
In late December 2003 and early January 2004, I made additional measurements of loading inductor currents. The results clearly agree with the analysis that had been presented on this page since early 2003. Without displacement currents, currents into and out of a loading inductor are equal. That is a hard rule, it agrees with theories defined by people much smarter than me, and I believe it is unbendable unless the works of Faraday, Maxwell, Ohm, and Kirchhoff were incorrect.
A sample of measurements above and below the loading coil with various antenna above the coil (current as percent of reference) follow:
| Toroid with hat | Small 2x2" coil with 24" hat up 24" | Long 12x3" coil with 24" hat up 24" | Long 12x3"coil with 6' whip | |
| Current below | 100% | 100 | 100 | 100 |
| Current above | 100 | 94.4 | 73 | 76% |
| Toroid with whip | long 12x1.5" coil with 6' whip | long 12x1.5" coil with 24" hat | Small 2x2" coil with 6' whip | |
| Current below | 100% | 100 | 100 | 100 |
| Current above coil | 100% | 79% | 75% | 96% |
| Current in whip 1ft above top of coil | 73% |
The most revealing thing was how noticeably small changes in stray capacitance near the middle and top of the loading coil affect current distribution. It was quite evident hanging a large meter on each end of the coil would greatly perturb the system.
Clearly we do NOT want:
- A large hat just above a large coil
- A long large coil and a short whip
- A coil near large sheetmetal
More data along with photographs will appear on a new page over the next month or so. Until then, I can assure everyone the conventional theories presented below are accurate, and the theory that "electrical length" the coil "replaces" is incorrect. Loading coils indeed behave like any other inductor in the world.
Independent measurements by a reliable engineer have agreed with my measurements above. Anyone doubting my data need only read the following e-mail from W7EL.
The Incorrect Assumption
Another commonly misconception is, since voltage increases at the far end of the loading coil, current must logically decrease. After all, we have a fixed amount of power and voltage has increased. The assumption is:
1.) We multiply voltage times current to get power.
2.) If voltage increases current must decrease.
Unfortunately, this is not correct in reactive systems! Simple P (power) = I (current) times E (voltage) only works when the system is non-reactive. This condition only occurs at resonance, and only below the loading coil at the antenna feedpoint!
In a reactive system, like in a mobile whip above a loading coil, voltage and current are no longer in phase. As a matter of fact, voltage and current can closely approach being 90 degrees out-of-phase when the whip is electrically very short. Since the antenna area above the loading coil is highly reactive (voltage is not in phase with current), we can not multiply voltage times current without considering phase differences.
You may have heard the term "reactive power" or VAR (volt-amperes-reactive). Reactive power is voltage times current without consideration of phase angle. We can have kilowatts of VAR power with only a low power transmitter, and that is what we actually have in the reactive part of the small antenna.
Coil Q and Changes in Efficiency
Current taper or reduction has been cited as a reason coil "Q" has little effect on signal level in mobile systems. Speculation is only the first few turns of the loading coil carry significant current because the coil "leaks" magnetic fields and radiates, and this is why the coil Q has little effect.
Another idea proposes the loading coil "makes up" a certain missing part of the antenna. It goes on to conclude the loading coil can be accounted for in "electrical degrees", making up the "missing difference" in antenna degrees. This isn't true either. The inductor doesn't know where it is and suddenly change from "x" ohms reactance to electrical degrees! It responds to AC currents and voltages as any inductor in any circuit does. It doesn't suddenly change measurement units.
As an example of this, try to define a 45-degree electrical length inductor at 1.8 MHz. That would mean it is a capacitor at 3.61MHz, where it is over 90-degrees long! How many turns at what length and diameter is a 45-degree inductor?? Where is a formula that allows converting a given size inductor to electrical degrees? This shows how useless and meaningless that definition is!
The inductor adds a certain amount of series reactance, that's all. A 300uH inductor is not 20-degrees long, nor is it 80-degrees long, so far as radiation goes unless it is really that long physically. It is a certain number of ohms reactance at a certain frequency, or a certain number of units called Henries. It is not "electrical degrees" that it adds, it is a non-dissipative reactance (in combination with a loss resistance because of finite quality) at a certain frequency!
A loading inductor can "insert" a large amount of phase shift, but the phase shift is between voltage and current. The only exception to this would be if the inductor had considerable distributed shunt capacitance to the outside world, and acted like a string of series inductors (with the antenna) and shunt capacitors (shunting to the ground system). In that case we could expect coil Q to be extremely low, since it would be the electrical equivalent of a lossy transmission line. That's either an awful loading coil, or it is a less-efficient helical loaded antenna!
The Correct View
Another group of people don't argue against established and proven circuit theory. They understand charges flowing into one end of the loading coil must have someplace to branch off (a virtual third terminal), or they must flow out the other end. Without that additional "virtual" path, charges flowing into the coil would always equal charges flowing out. This is true regardless of radiation, losses, or induction fields.
This makes perfect sense when we think of any dc circuit, antenna, or RF system. Electrical rules are satisfied, the system behaves as it does in the real world.
There is very little change in current, unless the coil is physically very long compared to the rest of the antenna above the coil or unless the coil is laid right against "grounded" conductors and the whip above the coil is very short. This fits perfectly with helical verticals, where the coil is "stretched out" over the length of the antenna.
It also agrees with base loaded antennas, which have nearly as much current into the antenna above the coil as at the feedpoint. It agrees with center loaded antennas, where current below the coil is essentially uniform and the whip above has triangular distribution.
Current can be different in various areas of an inductor, but only if shunting capacitances (impedances) to the outside world are significant compared to load capacitance (impedance). Another condition where current can vary substantially is with operation near the condition of self-resonance in what is normally considered or defined as a "series-resonant" mode. This would be a very poor and inefficient loading inductor, such as when a 160-meter antenna is used at a secondary resonant frequency in upper HF.
Circuit Model of a Mobile Antenna

This model represents what might be a typical mobile antenna installation if the coil is compact and has very good flux coupling through the length of the coil.
- Rgnd ground resistance of vehicle normalized to feedpoint
- V1 coaxial feed line
- C2 base capacitance
- Rrbase Radiation resistance of the base area of the antenna
- L1 loading coil
- Rcoil coil equivalent series loss resistance
- C3 coil shunt C to ground
- Rr top area radiation resistance
- Cant equivalent antenna capacitance above coil area
My 160 Mobile Antenna
I've worked all continents except Africa while 160-meter mobile. I have CW contacts at over 10,000 miles, and SSB as far as Europe (4000 miles). My mobile antenna consists of an eight- foot antenna with a six-foot hat (made from surplus Ford or Chrysler car antennas) at the top. The loading coil is at 5 feet.
This antenna has been on the truck for thousands of miles, without mechanical failure. It is mounted at the upper left corner of the truck bed, about one foot back from the cab.
The following is a model of the current antenna system on my Ford F-250 HD long bed super cab truck:
The base impedance in the model is:
Frequency = 1.854
MHz.
Source 1 Voltage =
24 V. at 2.35 deg.
Current = 1 A. at
0.0 deg.
Impedance = 23.98 +
J 0.9853 ohms
Power = 23.98 watts
SWR (50 ohm system)
= 2.087
Actual measurement at my Johnstonville, GA farm in open flat pastures on August 17 at 8AM. Wet soil 25.8 ohms 0j base impedance, pretty close agreement to EZNEC model and earlier data! (I did have to adjust the model for very low ground conductivity, otherwise the resistance was far too low. It's my belief that NEC-2 underestimates ground losses in small radial or counterpoise systems that are close to earth.) Earlier text shows a base resistance of 28 ohms, that was dry soil with a slightly different loading coil and antenna.
The modeled current distribution for 1-ampere applied at the base (in 1-foot intervals) is:
1ft=
1.0031
2 ft= 1.0091
3ft= 1.0178
4ft= 1.0318
<Coil>
5ft= 1.0175
6ft= .97512
7ft= .92984
8ft = .89522
Measuring the current into and out of the loading coil with a small thermocouple RF meter, I detect no difference This is in close agreement with the model.
The efficiency of this antenna knowing coil Q, radiation resistance, and base resistance calculates just under 1 percent. The model indicates about 1/3 percent efficiency. This is reasonably close.
Removing the hat (in the model only) shows the following changes:
1ft = 1.0043
2ft = 1.0133
3 ft= 1.0279
4 ft= 1.0566
<coil>
5 ft= .95508
6 ft= .72232
7 ft= .27813
8 ft = open
I haven't tested the above, but with the same loading coil loss resistance the model says efficiency is now around 3dB worse. Removing the hat, with NO change in coil resistance, shows nearly loss nearly doubles. Of course the coil resistance would increase, because the loading coil nearly quadruples in size. Bandwidth is less and efficiency is less, even if I could maintain the same coil resistance.
Examples of Unequal Current
In the above models, we see that current into and out of the one-foot long coil is about the same. There is only about 2% change in current even though the coil occupies 12% of antenna length in the "hat-loaded" antenna, but in fairness I couldn't resolve that change with a reasonably good RF current meter.
The model predicts 10% change in a non-hat antenna, but I never measured that antenna to confirm it.
Clearly there is no basis to the claim current is high only in the first few turns of an inductor, or that current tapers in relationship to "electrical degrees". The most accurate way to state the effect would be to say: "When the loading coil is short and the capacitance of the antenna beyond the coil is reasonable (in this case 3000 ohms Xc or less), there is an immeasurable reduction in current in the coil. When the required loading reactance is very high (in this case 8000 ohms), the reduction in current is about what we would expect for an equivalent length of antenna replacing the coil."
Degrees Vs Radiation Resistance
This upper four feet of this antenna resonates near 24 MHz with the hat. We can assume it is 90 degrees long at 24 MHz, which would translate to 6.9 degrees on 1.85 MHz. Following that same logic, this would mean the loading coil would be about 83 degrees long electrically. Using the incorrect logic proposed by others where the loading coil "makes up the difference in electrical degrees", there would be almost no current past the loading coil. Obviously this is not the case, the loading coil has very little "electrical length". As a matter of fact, in this case because the inductor is terminated in a fairly low capacitance and the inductor is compact with good flux linkage through all the turns, electrical length is much closer to the physical length of the coil than the "missing antenna length" in degrees!
This goes back to radiation theory, and my favorite saying: "Five hundred feet of wire in a one foot long tube is still one foot of antenna". Some CB manufactures sell antennas to consumers with the claim they use 5/8 or 3/4 wavelength of wire in an eight-foot fiberglass whip, so the antenna has more gain. Obviously this is not true. Let's not let such silly claims spread into amateur radio!
Related topics:
The spice inductor model shows one example of how unequal current is created. The model demonstrates a coil having significant distributed capacitance to the point of current return in the system compared to terminating impedance of the coil. In a monopole this return path would be to the groundplane, or anything closer to the potential of the groundplane than the area above the loading coil's position in the antenna system.
Another Practical Antenna Example
Let's assume we have a lossless 15.3 foot long 0.2 inch diameter conductor over a perfect groundplane. Eznec gives the 1.821 MHz base impedance as .3004 -2169j. In other words, the antenna "looks like" .3004 ohms of load resistance in series with 40.32pF on 1821kHz. The return path for current is through the .3004 ohm resistance and 40.32pF capacitance, back to the ground of the antenna (it is a Marconi antenna).
Such a termination (load) would require a series inductance of 2169j (189.57ÁH) to cancel feedpoint capacitive reactance. A typical 190ÁH inductor would be rather large, requiring somewhere around 53 turns when using a 4" by 4" form factor. One would expect a physically large inductor to have noticeable but very small displacement currents to the groundplane, when the small stray coil capacitance is compared to the 40.32pF termination capacitance. This raises two very important design guidelines:
- When installing a loading coil of substantial inductance in an electrically short antenna, sheetmetal and dielectrics should be kept away from the coil and areas of antenna above the loading coil. This would include dielectrics on or near the inductor, since the presence of dielectrics would increase undesirable capacitance.
- When inductive reactance requirements are large, as when short thin "stingers" without hats are used above a coil, the coil form factor should lean more towards long and thin. Capacitances near the open end of the coil (high voltage end) should be minimized. This would be true even when the coil length increase results in a small reduction in mutual turns coupling, since the stray capacitance may result in a larger loss penalty than the slight increase in accumulated resistance from additional wire length.
Efficiency
Efficiency in any antenna near earth is almost always dominated by ground related losses, short-height Marconi antennas are no exception. The overall effect of loading inductor Q and matching system losses are "diluted" or "swamped-out" by ground losses. Ground losses cause most systems to have greatly reduced sensitivity to inductor design.
The only consistently predictable factor in efficiency in fractional wavelength Marconi antennas with limited size ground systems is radiation resistance. Efficiency increases almost directly in proportion to radiation resistance.
Radiation Resistance and Power Radiated
Radiation resistance is probably the most poorly defined term used with antennas. The lack of clear definition creates errors and misjudgments when predicting antenna performance. If you wish more detailed information, this page contains information on radiation resistance. For the purposes of this discussion and to avoid pitfalls associated with using feedpoint impedance as radiation resistance, I'll use the same definitions Jasik, Balmain, and others have used. This definition is based on the IRE definition of radiation resistance being equal to the net or effective current causing radiation squared divided by the power radiated as EM energy, or Rr=Pr/I^2.
Using this definition, a folded dipole has a radiation resistance identical to a conventional dipole of the same physical dimensions ( ~70 ohms).
Radiation is caused by charge acceleration, there is no magic. The only thing affecting radiation resistance in a short vertical antenna near ground is current distribution over the linear area occupied by the radiation portion of the antenna. The general rules are:
Radiation resistance of a Marconi vertical in the maximum possible radiation resistance case for a given height (this is the case where current is uniform throughout the structure) is equal to 1580*(H/L)^2 where H equals height and L equals wavelength and both are expressed in the same units. Using degrees, we see a 10-degree tall antenna has a maximum possible radiation resistance of 1580*(10/360)^2 or 1580*.000772 = 1.22 ohms. This would apply even if the antenna is a vertical, DDRR, Fractal, or folded unipole with considerable top loading.
If current is triangular, radiation resistance would decrease by a factor of four to 0.305 ohms.
Power radiated is given by I^2*Rr
With 100-watts applied to a 10-degree tall antenna, net current in a lossless antenna with uniform current distribution would be 9.05 amperes. With triangular distribution, such as appears in a small diameter short base loaded whip, current would be approximately 18.1 amperes. We are in serious problems if the inductor reduces current along its length, since the only possible way to radiate 100 watts would be to have somewhere around 9 amperes of effective current integrated over the 10-degree vertical area of space for the radiator!
Ground Losses
All current flowing (or displaced) vertically into the antenna must equal current flowing out of the ground or counterpoise system. Even though ground losses are distributed losses, we must normalize all losses to the feedpoint in order to compare systems. There are cases where this will not always occur, causing us to falsely assume we have lower losses than really exist.
In this tutorial and comparison, I have normalized ground losses to the same point where radiation resistance is considered.
System Losses
(Measured data below of actual antenna given below was from 1995 data taken at a different location near Atlanta with a slightly different loading coil and antenna. There is a slight disagreement with current data. I left this all in so you can see the departure from measurements and models using 8 year old data.)
Base Loaded (Triangular Antenna Current Distribution) with no ground loss
Assuming we have a base-loaded antenna, and the operating frequency has a wavelength of 550 feet (around the 160-meter band), a 15.3 foot vertical would fit the above 10-degree value. Interestingly enough when we compare Eznec to formulas available in older (1950 vintage) engineering textbooks, we find radiation resistance predicted by Eznec is .3003 ohms while the triangular current estimate for the same height radiator is .305 ohms! This is an amazing degree of agreement, illustrating what we could do before modeling programs became available. (With perfect top loading, both Eznec and longhand calculations show approximately 1.2 ohms of radiation resistance.)
Assuming our 15.3 foot tall (10-degree) base-loaded antenna uses a coil Q of 200, the coil has 10.845 ohms of ESR. Total resistance with a perfect ground would be 10.85+.3= 11.15 ohms. Current into this system with 100 watts applied would be around 3 amperes, resulting in ~2.7 watts radiated and ~97.3 watts lost as heat in the inductor.
Doubling coil Q (400) would provide 5.73 ohms of base resistance with 4.18 amperes. Power radiated would be 5.2 watts, power lost as heat would be 94.8 watts. Efficiency does not quite double, changing from 2.7 to 5.2%. This results in a 2.8dB change in signal level.
Top Loaded (with no ground loss)
If we added a four-wire hat with 15-foot wires, current would no longer be triangular. While we wouldn't quite reach the optimum uniform distribution, current at the top would be about 78% of current at the antenna base. Feedpoint impedance would become 0.97 -551j, and the antenna would look like 0.97 ohms in series with 159pF.
Using a coil Q of 200, we would now have 2.76 ohms of inductor loss. Current becomes 5.18 amperes. Radiated power is 26 watts, while power lost as heat becomes 74 watts. Even in the perfect ground case, the change in efficiency caused by top loading is large. Top loading (with only the hat) results in 9.8 dB change in signal level when compared to the base loaded case when coil Q remains 200. Efficiency is 26%. The coil remains at ground level for easy matching and frequency change.
In this case current at each terminal of the loading coil would be essentially the same regardless of poor coil mounting techniques. In order to have significant current taper in the coil or in the bottom of the mast, shunt capacitance would have to be a significant compared to 160pF. The antenna's high input capacitance relaxes inductor and antenna mounting electrical requirements.
Base Loaded (high ground loss)
My F-250HD Super Cab pickup truck, when parked over open medium quality pasture land, has a ground resistance of about 20 ohms (normalized to the feedpoint) on 160 meters. Applying this ground loss to the base loaded antenna, the system has a feedpoint resistance of 20+.3=20.3 ohms. (This is reasonably close to actual feedpoint resistances measured with a similar operating antenna.) Adding coil losses, the system has 20.3+10.85=31.15 ohms. (NOTE: Current coil is ~8 ohms ESR, 10.85 ohms is from ~8 year old data) Current is sqrt (100/31.15) or 1.79 amperes.
This results in .96 watts radiated, and 99.04 watts lost as heat. Efficiency is now around .96%.
Substitution of a coil with a Q of 400 results in 25.7 ohms feed resistance, or 1.97 amperes antenna current at 100 watts. In this case efficiency is now 1.16% for 1.16 watts radiated. The change caused by doubling coil Q with high system ground losses is about 0.8dB, compared to almost 3dB in the perfect ground case! With a poor ground (in this case typical of a very large vehicle), a large change in coil Q produces little change in system efficiency.
Another Top Loaded (high ground loss) System Example (made prior to the EZNEC model above)
Using a large hat isn't practical in a moving mobile, although it could apply to fixed stations suffering with poor ground systems. When the hat is smaller, such as a mobile requires, the loading inductor can be moved higher in the system. Such a move would produce uniform current below the loading coil, with a current shape above the coil dictated by the construction of the upper portion of the antenna. My own mobile uses a six-foot diameter hat manufactured from stainless steel automobile antennas arranged in a spoke. I have no problems with wind or occasional obstructions. While unsightly, a modest hat is workable.
In order to keep the systems comparable I'll use the same radiation resistance provided by a large hat, but intentionally add high ground loss as a lumped resistance. This model ignores field losses near the antenna.
In this case we have 0.97 -551j as the inductor termination presented by the antenna. With ground losses normalized at 20 ohms and an inductor Q of 200, we have 20+2.76+.97 = 23.73 ohms of feedpoint resistance. Current is 2.05 amperes, and power radiated is 4.1 watts. Power lost is 95.9 watts.
Efficiency is 4.1%, a 6.3dB increase over a base-loaded triangular current system with the same lossy ground. This system is 8dB down from the same "top-loaded" distribution using a perfect ground.
When the system has significant fixed losses, increasing radiation resistance four times by top loading provides a similar dividend in system efficiency. At the same time a substantial increase in coil Q provides only minimal change in field strength.
Current Through Coil
Related pages:
There has been some speculation that current is high only in the first few turns of a loading inductor. Radiation comes solely from charge acceleration or current over spatial (in line) distance.
If any loading inductor shows substantial decrease in current over the length of the inductor, it is an absolute certainty that the inductor is poorly designed and that the system above the loading inductor is not contributing to system efficiency. The reason for this is very simple and straight forward. Any two-terminal component (even considering wire as a "component" applies) MUST have equal charges flowing into and out of each terminal. Voltages to other reference points can be different, but for every charge moving into one terminal a like number of charges MUST move out of the other terminal. Radiation, induction fields, and loss resistances have no influence on this rule.
In order to have any change in current, there must be an additional path or paths for charges. This path can be through leakage resistances, or through fictitious currents called displacement currents. Whatever the path, the total charge movements must be reconcilable. We simply can not have current "disappear".
The normal path upsetting "unbalancing" current into and out of each terminal in an inductor is provided by displacement currents through electric fields. As with any system, the amount of current flow is proportional to potential difference and impedance of the path. In order to shunt a substantial current out of an inductor, the potential difference between the ends of the path has to be high compared to the impedance of the path. The impedance of the stray path must also be reasonably low compared to the normal desired path.
Current diversion is problematic in very large inductors operated at (or very near) internal self resonance, when the self resonance is what we typically refer to as a "series-resonant" condition. This condition is common in plate chokes used in vacuum tube power amplifiers, where the system operates over many octaves of frequency range.
"Series resonances" inside components occur when distributed inductance forms a pair (or multiples of pairs) of "L" networks. The large series inductance from each end of a winding reacts with the small stray capacitance at the center, and forms a very high impedance transformation L network. The electrical potential at the center of the system becomes extremely high, and even the smallest amount of capacitance to surrounding objects will carry a substantial displacement current. The large displacement currents cause the terminal impedances to drop, and allow considerable current to concentrate in small areas of the component. At the same time, considerable voltage can be present. The normal result is arcing or destruction of the component, or failure of the system depending on the choke to operate.
Series resonance always occurs at a frequency higher than the self parallel resonant frequency of the component. A loading coil operating under such conditions would be required to have serious design errors to fall into this category, since the end termination capacitances should always be substantially higher than stray capacitance throughout the component. Failure to follow this rule would result in needless loss and reduced SWR bandwidth in an antenna.
The speculation or supposition that the first few turns of a loading coil carry most of the current is clearly untrue. In order to shunt current off, high series impedances would have to exist along with high stray shunting capacitance to areas removed from the radiator. Additionally, the remaining coil area connected to the top area of the antenna above the loading coil would have to present a high impedance to the area where current reduction occurs. This would never be the case, unless the top area of the antenna and loading coil are not resonant near the operating frequency.
A reasonable test for proper inductor and system design would be to remove the antenna above the loading coil, measuring system resonance. If resonance does not change substantially, the area above the coil is not correctly terminating the system. First-order self resonance of the inductor (parallel resonance), when removed from the system, should also be far above the operating frequency of the system. If self-resonance comes within three or four times the operating frequency range, the loading coil almost certainly will have needless performance shortfalls.
Conclusion
A normally functioning inductor has essentially equal currents throughout the inductor, loading coils are no exception. Any current difference requires "missing current" flow through undesired stray capacitances (displacement current) or leakage currents.
In a reasonably well-designed system, current into and out of the loading inductor should be substantially equal. Large differences in current would indicate excessive and problematic undesired stray capacitance in the loading coil or antenna system design.
Reduced sensitivity to coil Q is primarily a function of additional losses in the system, not reduction of current through the coil.
Also see Loading Inductors
This page
has had
visits
since February 11,
2004.