Omega's and Gamma's
Impedance Limits
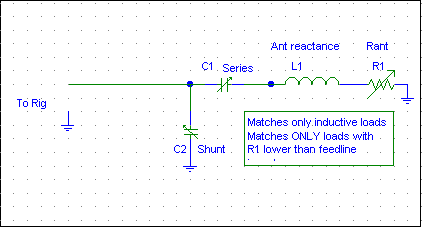
The best matching system for feeding a grounded Marconi element, unless we are very lucky or very careful in planning the installation, is a simple gamma capacitor and shunt feed conductor with the tap point adjusted to find 50 ohms resistive.
While losses are not significantly increased when using an Omega match with reasonably sized components, matching range is not significantly extended either! At best, the Omega match saves us a few trips up and down the tower while searching for the precise shorting strap position between the gamma wire or cage and the tower. If we are already at the top of a tower with the gamma tap point, and if at that point we find resistance (after reactance is cancelled by adjustment of the gamma) is too high, an Omega will not help. The Omega can only match loads LESS than 50 ohms resistive by stepping the resistance up! It can NOT step or transform antenna feed resistance downwards when using capacitors, and neither the Omega or Gamma can match capacitive antenna loads.
By adding an inductor, we can greatly extend the matching range. The extra time, expense, and complexity of adding a high-Q inductor would not offset the slight reduction in effort to simply find the correct shorting point for gamma and omega capacitor systems.
Gamma Match
The gamma match capacitor can only cancel reactance, it can not modify the "real part" (resistance) presented to the feed line. It is the most simple form of matching, and has the lowest operating Q and loss of any system (when it is useable). Adjustment of resistance (real part) requires adjusting the diameter, spacing, or length of the gamma section.
The voltage rating of the capacitor is simple to find. It is Y*I*X where Y is the safety factor and adjustment for peak voltage (RMS*1.414), I is the RMS current from the feed line, and X is the reactance (in ohms) of the capacitor. Y is normally a factor of four to allow for peak conversion, SWR, component flaws, and transients.
The current rating is simply the RMS current plus a safety factor. Component physical size as well as Q control the current rating. See component ratings.
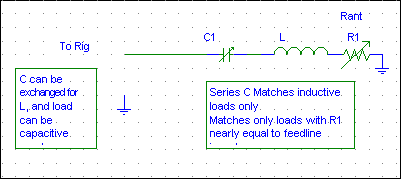
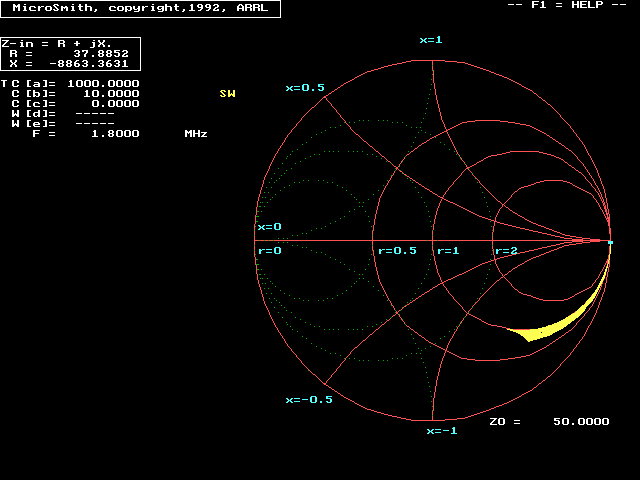
Looking at a Smith Chart, we see a single line (yellow) following a portion of the resistance circle with a resistance value of 1 (1 is normalized to 50 ohms). The gamma match can not deviate from that resistance circle, and so the resistance must be adjusted or transformed by other means. We normally adjust the gamma system's tap point by using a movable shorting strap to change R. Just moving a short is enough, it is not necessary to remove the extra "unused" portion above or beyond the shorting strap.
Let's consider a 1500-watt transmitter and 50-ohm
transmission line, with a 1:1 VSWR. The matched line current is found using ![]() . The result is 5.5a RMS current.
. The result is 5.5a RMS current.
With 1500 watts and 50 ohms we have 5.5 amperes RMS. Assuming
the match requires 300pF at 1.8MHz we have: ![]()
4*295* 5.5 = 6490 volts. It's easy to see why arcing is a problem when capacitance is low! Very few air variables would take such a high voltage, and insulators (especially when exposed to moisture) also become a problem. This is typical of a shunt-fed element when the matching section is a thin long wire.
We can decrease reactance by increasing the effective diameter of gamma conductors, and this will increase required capacitance value. One way to decrease reactance is to use a cage of wires spaced as far apart as possible. Halving the reactance (doubling the capacitance value) will cut peak voltage in half, with no other changes. This has the effect of quadrupling the power rating when using the same breakdown voltage ratings in components!
A thicker gamma conductor also lowers operating (loaded) Q. This is a series-resonant system, operating Q is set by the amount of reactance in series with the load resistance (50 ohms). Reducing operating Q has the effect of increasing bandwidth while simultaneously reducing loss and increasing power rating.
Note that bandwidth increased while efficiency increased. This happens in many cases. Popular folklore tells us narrow antennas are efficient, but that is true only in a few specific cases. In most cases, bandwidth by itself tells us nothing about system efficiency!
One example of a conundrum with gamma capacitors is found in yagi antennas. If we increase capacitor dielectric thickness by decreasing inner rod size, the voltage across the capacitor can actually increase at a faster rate than insulation thickness increases! The same is true if we increase gamma capacitor length in an effort to restore capacitance after increasing outer conductor diameter. The effect thicker insulation and higher voltage rating, if done incorrectly, can be to make little change or perhaps even decrease gamma capacitor power rating!! Always use a large diameter gamma rod, and increase the dielectric thickness ONLY by increasing the outer rod to accommodate dielectric thickness changes. At the same time, the inner rod should be increased to avoid any requirement of making the gamma capacitor longer. Avoid sharp points or edges on the rods, just as you would avoid sharp points in any HV system....especially inside the "capacitor".
The above example of decreased power rating is especially important to Amateurs using coaxial cables as capacitors. Voltage is NOT constant along the length of a long coaxial capacitor. Maximum voltage in the component is always HIGHER than the actual voltage across the terminals of the "capacitor", and it is higher than the voltage calculated by the current through the capacitor! Coaxial capacitors or linear stubs used as reactive elements always have significantly lower operating Q, higher power loss, and operate under more electrical stress than a well-designed lumped component. Stubs and linear loading does have the advantage of spreading heat out. You won't notice the heat as much, even though there is a lot more heat energy! Just don't let the smaller temperature rise fool you into thinking the system has less power loss.
Omega Match
The Omega Match is really just a form of the simple L-network.
Traditional Cs/Cp Omega Match
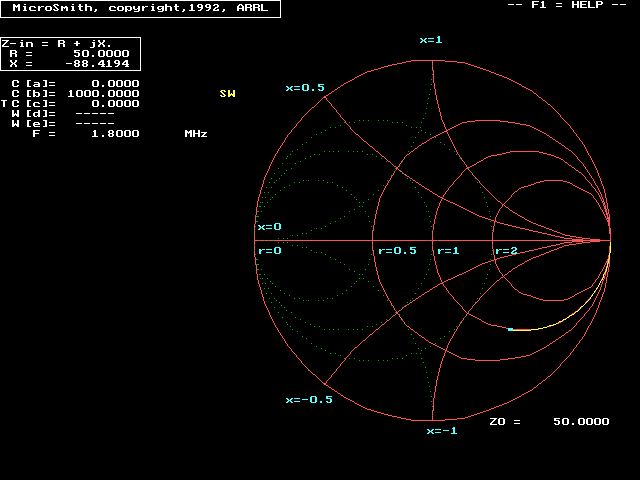
In this system, C2 parallels the shunt terminal and primarily sets the resistance transformation C1 is in series with the feed line, and primarily cancels reactance. If we look at this network on a Smith Chart, we see the resistance range is somewhat expanded over a conventional Gamma Match.
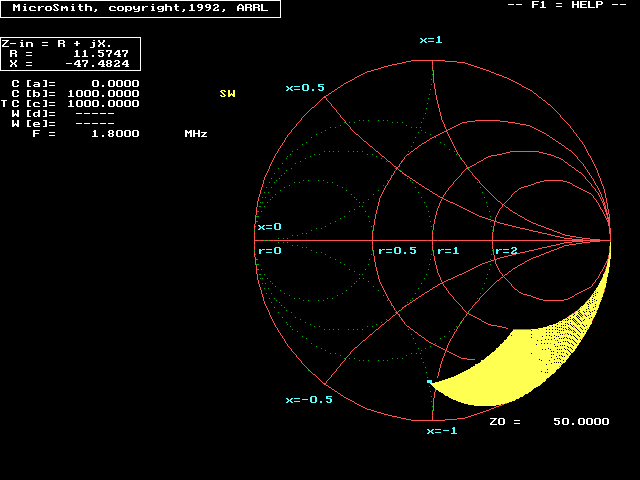
We also can see it is not the panacea often claimed. Look at the "r" circles on the above chart. "r=1" is normalized to 50 ohms. With that in mind "r=2" is 100 ohms, while "r=0.5" becomes 25 ohms. The Omega's resistive matching range, using 1000pF vacuum capacitors, would only from 50 ohms downwards. Voltage ratings are still a problem when the system requires capacitor C1 to have a small capacitance value (high reactance), and now we have two capacitors that have to handle essentially the same high voltages when C1's operating capacitance value is small!
This arrangement once again requires antenna shunt wire impedance to be lower than feed line impedance. The network, since it only uses capacitors, must be used with inductive loads or the feed line terminal will be reactive.
One useful application of this circuit is in matching very short non-resonant vertical element, sometimes called a "Hairpin Monopole". Well-designed capacitors, such as vacuum capacitors, have such high Q they are essentially lossless. With vacuum capacitors and very good connections, losses in the matching system are very low even with very high currents. We shouldn't be misled into thinking we have a "free-lunch" magical short antenna! We "pay for our meal" in greatly increased conductor losses in the antenna conductor. The conductors not only carry common-mode radiation currents, they also must carry significant circulating currents involved with the feed-system. These high currents causes distributed conductor losses to be much higher than conventional loading systems using a reasonable-Q lumped inductor. Bandwidth and radiation resistance for a given element size is often significantly less than conventional series-feed when using a hairpin monopole with Omega loading and matching, although the system has the advantage of being easily tuned to new frequencies. The Omega/hairpin vertical also allows the feedpoint resistance to be adjusted to nearly any value we might require.
C1 is primarily for power factor (reactance) canceling. It is rated exactly as in the gamma, voltage and current being determined by the required amount of operating reactance and the line current.
C2 primarily sets resistance transformation. The component's electrical requirements are found only by knowing the load impedance and the reactive voltage and current in that branch of the system. It handles a portion of the input current, as well as a portion of the shunt current, so the current in C2 is always higher than the current from the source flowing through C1. The required voltage rating of C2 is also always higher than C1.
Assuming we have 10-1000pF variables, the normal matching range covers inductive reactance ranging from 80 to 4000 ohms with a resistance between 1 and 50 ohms. Lower reactances are only able to be tuned when the resistance is near 50 ohms. As you can see, resistive matching range is wide but limited to values below 50 ohms.
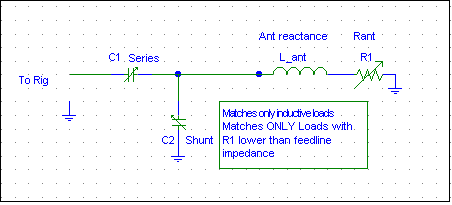
Cp/Cs Omega Match
The parallel-C input, series-C output is also a form of the L-network. The output, once again, must be the lower impedance while the feed line must have the higher impedance. Once again, this system only matches inductive loads.
It is not a very useful circuit, except in specific applications. The only advantage of this arrangement is C2 operates at significantly less voltage. The voltage across C2 is always no greater than the transmission line voltage, larger receiving-type air variables will operate at 1500-watt and higher power levels. Because C2 is under significantly less electrical stress, It is the better choice if you are very close to having a match and only need adjust resistance upwards slightly for perfect match.
C1 primarily sets reactance, while C2 primarily sets resistance.
Assuming we have 10-1000pF variables, the normal matching range is reactances up 8000 ohms inductive and resistances between 38 and 50 ohms. As you can see, resistive matching range is very limited. C2 would need to be a very large capacitor (very low reactance) to have a wider resistance range.
Pi Matching
In cases where we can not find a 50-ohm tap point, we can add an inductor. In this case C1 can be a fixed or variable capacitor capable of handling modest voltage and current, such as a snubber-mica or receiving-type air variable.
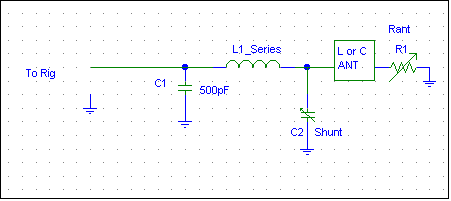
L1 has to be fairly large to match high resistance and reactance ratios, at least 100uH on 160 meters for the extremes shown in the Smith Chart below. Assuming a 10-1000pF capacitor for C2, a 500pF capacitor for C1, and a 100uH adjustable inductor for L1 we would have the following matching range:
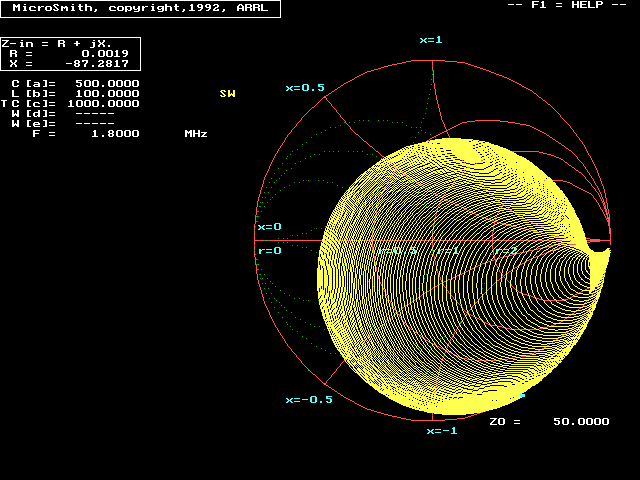
Matching range is greatly extended, and even covers capacitive loads.
Power Ratings
Heating is a long term problem that accumulates with time.
Failure occurs when the heat causes a component to physically change from
excessive heat. Heating is related to power dissipated by a simple formula
![]() The
resistance is normally determined by knowing the component's Q (not the
operating Q) and the current through the component.
The
resistance is normally determined by knowing the component's Q (not the
operating Q) and the current through the component.
The series resistance that dissipates energy as heat is found by dividing reactance by component Q. With 88 ohms and a Q of 5000 (typical of a good large air capacitor) Equivalent Series Resistance is 88/5000 or .0176 ohms. Heat is given by .0176 squared times 3.11 amperes. Heat is .0176*3.11*3.11 or .170 watts, not bad for an air variable capacitor. (Multi-layer chip capacitors can have Q's in the tens or hundreds of thousands, as can vacuum capacitors. Simple ceramic disc and small mica capacitors generally have Q's in the upper hundreds to many thousands.)
Current through C2 is found by dividing 274 volts by R-ant. If R-ant were 15 ohms the current would be 274/15 or 18.27 amperes. Voltage would be C2's reactance of 88 ohms times 18.26 amperes times the safety and peak factor of 4. Peak voltage would be 6500 volts for an 88-ohm reactance capacitor. This is a good example of why "T" antenna tuners arc with low load impedances while working fine at higher impedances, and handle more power when tuned to use maximum possible capacitance.
Arcing is an instantaneous voltage problem. In general a solid dielectric (insulation) punches through and fails almost instantly. Voltage rating is reduced with every arc, even brief unnoticeable arcs. As a general rule solid dielectrics suffer non-recoverable damage from any arc, even a very brief arc (such as a momentary low-current static discharge.
If the dielectric is a vacuum, liquid, or gas, and if the component's conductors or dielectric do not physically distort or change from heating, the insulation can "heal" and full performance is often restored. With an air capacitor, ionized air must circulate out of the capacitor.
If an arc causes a physical change, such as a hole, carbon path, sharpened or raised edge, breakdown voltage is almost always permanently reduced. One exception would be when an arc removes debris or sharp points, such as melting copper whiskers in a vacuum capacitor (copper can actually grow tiny whiskers in a high vacuum). Sharp points, even microscopic sharp points, greatly reduce breakdown voltage. If a sharp point is reduced and rounded by an arc, voltage breakdown will increase. If we actually melt the plate, voltage rating is reduced. Surfaces must be micro-polished, we cannot sand a capacitor plate to restore full breakdown levels if a capacitor is arc-damaged (variable capacitor plates are commonly polished by tumbling them in a very soft abrasive like walnut shells).
Capacitors in parallel with a known resistance. RMS sinewave voltage across
the component is given by ![]() where P= maximum possible level of PEP applied. R=resistance the capacitor
parallels.
where P= maximum possible level of PEP applied. R=resistance the capacitor
parallels.
Capacitors arc and fail from instantaneous voltage peaks, not from average or RMS voltage. We multiply the RMS voltage across C1 times 1.414 and add an important safety factor. Multiplying RMS voltage by four normally works for outdoor mounted air-capacitors, as long as they are kept debris and moisture free.
A 50-ohm feed line with 1500 watts of absolute peak power (1500 watts CW or FM carrier or 1500 watts PEP SSB or AM) applied results in 274 volts RMS times 4 or about 1.1kV. Use a 1.1kV or higher voltage variable. This would be about .030" air gap in a typical construction air capacitor with normal manufacturing irregularities (generally very safe to assume .01" spacing for every 300 volts). With 50-ohm matched lines and a 1500-watt PEP (or CW carrier) transmitter, smaller transmitting or larger receiving air variables will work.
Heating
Current through resistance causes heating. The resulting heat over some period of time can cause physical changes that physically alter the component. In the short term, this can change the electrical parameters such as capacitance or voltage breakdown.
To find electrical energy converted to heat, we have to know the equivalent dissipative parallel resistance and voltage across the component or the equivalent series resistance (ESR) and current through the component. I generally work with current and ESR.
The current is a function of reactance and voltage across the capacitor, just like current through a resistance is found from voltage across the value of resistance. Assuming we have 1500 watts and 50 ohms resistive load directly across the capacitor, we have 274 RMS volts across the reactance of C1. This voltage, over the reactance in ohms, gives us the RMS (heating) current flowing through the capacitor.
Use the formula I = E/X. With a 1000pF capacitor (88 ohms on 160m) we have 274/88 or about 3.11 amperes.
Note: This is not exact because capacitors have complex series-impedances, but it is close enough for our questions as long as we have reasonably good capacitors. One common exception where this simplification will not work is with long coaxial stubs. Long coaxial stubs have a considerable amount of distributed series inductance. This causes a voltage increase as we move away from the feedpoint in an open stub, or a current increase as we move out on a shorted stub. This increase in voltage or current increases loss, decreases bandwidth, and increases effective loss resistance. Not only that, a stub (or linear loading) has higher distributed resistance because it has long conductors, rather than thick compact conductor area like a conventional component.
Loss and Component Failure
We often gauge system "loss" by the temperature of the component. We often assume a "cool" feeling component has low loss and a hot feeling component has very high loss. Using "touch or feel" temperature without considering size and ability to transfer heat is a good way to estimate component life, but it is not a good way to estimate system efficiency or component losses. Unless we carefully consider the complex issue of physical size and ability to transfer or dissipate heat to surrounding objects or air, we will have no idea how much power is actually lost in the component. Small components not only get hotter, they get hotter much faster than large components!
A physically long coaxial capacitor has a large surface area to dissipate heat. Even a very lossy coaxial capacitor will have significantly less temperature rise than a small very low loss compact disk capacitor, because the capacitor concentrates all the heat into one very tiny area. We might form the impression we have an inefficient system because the small capacitor drifts in capacitance value or fails from heat, yet it is usually the cool-running stub that has much higher power loss!
This doesn't mean we shouldn't use a coaxial stub as a reactance if they are reliable, but it does mean we have to be careful assuming it is the best solution for loss.
Bandwidth
Bandwidth tells us nothing about efficiency, unless we understand the entire system in detail.
In general the largest bandwidth occurs with the fewest reactive components. Any unnecessary reactance will increase system operating Q. One exception is when multiple networks with low loaded (operating) Q are used to obtain a large phase shift, rather than a few components that would require high operating (loaded) Q.
Stubs act like a combination of many small series-inductances with multiple shunt-capacitors. Coaxial capacitors not only generally have more loss than reasonably-constructed lumped capacitors, they also have less bandwidth. A stub's reactance changes faster with frequency than reactance in a compact lumped component, because it contains "unnecessary" distributed reactances. The stub also has higher internal voltages and currents, because of the distributed reactances. A coaxial stub may be cheap and "feel cold" in operation, but we shouldn't delude ourselves into thinking it is less lossy than a small capacitor. Remember it isn't only power dissipated that determines temperature rise, we must consider the total area heat is distributed over. 1 watt of heat feels very hot in a component the size of a pencil eraser, while 100 watts of heat could be undetectable by touch in a long thick piece of coaxial cable!